题目内容
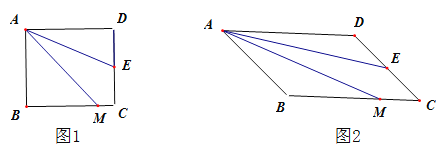
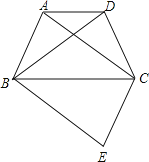
【题目】如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(1)求证:四边形ABEC是平行四边形.
(2)若AD=CD=6,∠ADC=120°,求四边形ABEC的面积.
【答案】(1)见解析;(2)36![]() .
.
【解析】
(1)由四边形ABCD为等腰梯形,AD∥BC,可得AB=DC,AC=BD,又由在平面内将△DBC沿BC翻折得到△EBC,可得EC=DC,DB=BE,继而可得:EC=AB,BE=AC,则可证得四边形ABEC是平行四边形;
(2)利用等腰梯形的性质,求得高和BC的长即可求得四边形ABEC的面积=2△ABC的面积.
(1)证明:∵四边形ABCD为等腰梯形,AD∥BC,
∴AB=DC,AC=BD,
由折叠的性质可得:EC=DC,DB=BE,
∴EC=AB,BE=AC,
∴四边形ABEC是平行四边形.
(2)解:如图,
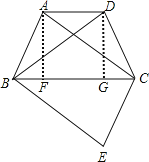
过点A、D分别作AF⊥BC,DG⊥BC,垂足分别为F、G,
∵AD∥BC,∠ADC=120°,
∴FG=AD=6,AF=DG,∠ABF=60°,
∵四边形ABCD为等腰梯形,
∴AB=DC=6,
∴BF=![]() AB=3,AF=
AB=3,AF=![]() AB=3
AB=3![]() ,
,
在Rt△ABF和Rt△CDG中,
![]() ,
,
∴Rt△ABF≌Rt△CDG(HL),
∴BF=GC=3,
∴BC=12,
∴S四边形ABEC=2S△ABC=2×![]() ×12×3
×12×3![]() =36
=36![]() .
.

练习册系列答案
相关题目