题目内容
【题目】等腰三角形的一个外角是 140°,则此多边形的三个内角的度数分别是________
【答案】40°,70°,70°或40°,40°,100°.
【解析】
因为已知的外角没有指明是哪个顶点对应的外角,故这个外角可以为顶角的外角,也可以为底角的外角,所以分140°为等腰三角形顶角的外角和140°为等腰三角形底角的外角两种情况考虑,根据邻补角定义分别求出外角的补角,然后根据等腰三角形的“等边对等角”及三角形的内角和定理即可求出其他角的度数,得到正确答案.
当140°为等腰三角形顶角的外角时,画出图形,如图所示:

根据图形外角∠DAC=140°,
∴∠BAC=180°-140°=40°,
又AB=AC,∴∠B=∠C=![]() =70°,
=70°,
则等腰三角形的三个内角分别为:40°,70°,70°;
当140°为等腰三角形底角的外角时,画出图形,如图所示:
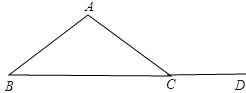
根据图形外角∠ADC=140°,∴∠ACB=180°-140°=40°,
又AB=AC,
∴∠B=∠ACB=40°,∠A=180°-40°-40°=100°,
则等腰三角形的三个内角分别为:40°,40°,100°,
综上,等腰三角形的内角分别为:40°,70°,70°或40°,40°,100°.
故答案为:40°,70°,70°或40°,40°,100°.

练习册系列答案
相关题目