题目内容
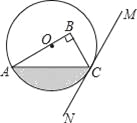
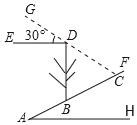
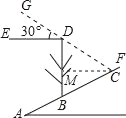
【题目】如图，斜坡AF的坡度为5：12，斜坡AF上一棵与水平面垂直的大树BD在阳光照射下，在斜坡上的影长BC=6.5米，此时光线与水平线恰好成30°角，求大树BD的高．（结果精确的0.1米，参考数据
≈1.414，
≈1.732）
【答案】大树的高约为6.0米．
【解析】
作CM⊥DB于点M，已知BC的坡度即可得到BM和CM的比值，在Rt△MBC中，利用勾股定理即可求得BM和MC的长度，再在Rt△DCM中利用三角函数求得DM的长，由BD=BM+DM即可求得大树BD的高．
作CM⊥DB于点M，
∵斜坡AF的坡度是1：：2.4，∠A=∠BCM，
∴
=
=
，
∴在直角△MBC中，设BM=5x，则CM=12x．
由勾股定理可得：BM2+CM2=BC2，
∴（5x）2+（12x）2=6.52，
解得：x=
，
∴BM=5x=
，CM=12x=6，
在直角△MDC中，∠DCM=∠EDG=30°，
∴DM=CMtan∠DCM=6tan30°=6×
=2
，
∴BD=DM+BM=+2≈2.5+2×1.732≈6.0（米）．
答：大树的高约为6.0米．
文敬图书课时先锋系列答案【题目】某公司销售部有营销员15人，销售部为了制定关于某种商品的每位营销员的个人月销售定额，统计了这15人某月关于此商品的个人月销售量（单位：件）如下：
个人月销售量 | 1800 | 510 | 250 | 210 | 150 | 120 |
营销员人数 | 1 | 1 | 3 | 5 | 3 | 2 |
（1）求这15位营销员该月关于此商品的个人月销售量的平均数，并直接写出这组数据的中位数和众数；
（2）假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件，你认为对多数营销员是否合理？并在（1）的基础上说明理由．
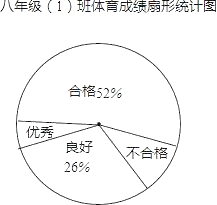
【题目】某校对九年级（1）班全体学生进行体育测试，测试成绩分为优秀、良好、合格和不合格四个等级，根据测试成绩绘制的不完整统计图表如下：
九年级（1）班体育成绩频数分布表：
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息，解答下列问题：
（1）九年级（1）班共有多少名学生？
（2）体育成绩为优秀的频数是 ，合格的频数为 ；
（3）若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛，恰好抽到1个男生和1个女生的概率是 ．
