题目内容
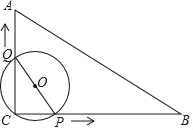
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2cm,AB=4cm,动点P从点C出发,在BC边上以每秒![]() cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C→A→B以每秒4cm的速度匀速运动,运动时间为t秒
cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C→A→B以每秒4cm的速度匀速运动,运动时间为t秒![]() ,连接PQ,以PQ为直径作⊙O.
,连接PQ,以PQ为直径作⊙O.
(1)当![]() 时,求△PCQ的面积;
时,求△PCQ的面积;
(2)设⊙O的面积为s,求s与t的函数关系式;
(3)当点Q在AB上运动时,⊙O与Rt△ABC的一边相切,求t的值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)t的值为
;(3)t的值为![]() 或1或
或1或![]() .
.
【解析】
(1)先根据t的值计算CQ和CP的长,由图形可知△PCQ是直角三角形,根据三角形面积公式可得结论;
(2)分两种情况:①当Q在边AC上运动时,②当Q在边AB上运动时;分别根据勾股定理计算PQ2,最后利用圆的面积公式可得S与t的关系式;
(3)分别当⊙O与BC相切时、当⊙O与AB相切时,当⊙O与AC相切时三种情况分类讨论即可确定答案.
(1)当t=![]() 时,CQ=4t=4×
时,CQ=4t=4×![]() =2,即此时Q与A重合,
=2,即此时Q与A重合,
CP=![]() t=
t=![]() ,
,
∵∠ACB=90°,
∴S△PCQ=![]() CQPC=
CQPC=![]() ×2×
×2×![]() =
=![]() ;
;
(2)分两种情况:
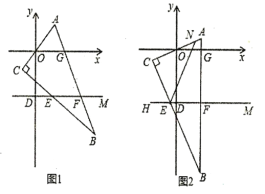
①当Q在边AC上运动时,0<t≤2,如图1,
由题意得:CQ=4t,CP=![]() t,
t,
由勾股定理得:PQ2=CQ2+PC2=(4t)2+(![]() t)2=19t2,
t)2=19t2,
∴S=![]() π=
π=![]() ;
;
②当Q在边AB上运动时,2<t<4如图2,
设⊙O与AB的另一个交点为D,连接PD,
∵CP=![]() t,AC+AQ=4t,
t,AC+AQ=4t,
∴PB=BC﹣PC=2![]() ﹣
﹣![]() t,BQ=2+4﹣4t=6﹣4t,
t,BQ=2+4﹣4t=6﹣4t,
∵PQ为⊙O的直径,
∴∠PDQ=90°,
Rt△ACB中,AC=2cm,AB=4cm,
∴∠B=30°,
Rt△PDB中,PD=![]() PB=
PB=![]() ,
,
∴BD=![]() ,
,
∴QD=BQ﹣BD=6﹣4t﹣![]() =3﹣
=3﹣![]() ,
,
∴PQ=![]() =
=![]() ,
,
∴S=![]() π=
π=![]() =
=![]() ;
;
(3)分三种情况:
①当⊙O与AC相切时,如图3,设切点为E,连接OE,过Q作QF⊥AC于F,
∴OE⊥AC,
∵AQ=4t﹣2,
Rt△AFQ中,∠AQF=30°,
∴AF=2t﹣1,
∴FQ=![]() (2t﹣1),
(2t﹣1),
∵FQ∥OE∥PC,OQ=OP,
∴EF=CE,
∴FQ+PC=2OE=PQ,
∴![]() (2t﹣1)+
(2t﹣1)+![]() t=
t=![]() ,
,
解得:t=![]() 或﹣
或﹣![]() (舍);
(舍);
②当⊙O与BC相切时,如图4,
此时PQ⊥BC,
∵BQ=6﹣4t,PB=2![]() ﹣
﹣![]() t,
t,
∴cos30°=![]() ,
,
∴![]() ,
,
∴t=1;
③当⊙O与BA相切时,如图5,
此时PQ⊥BA,
∵BQ=6﹣4t,PB=2![]() ﹣
﹣![]() t,
t,
∴cos30°=![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
综上所述,t的值为![]() 或1或
或1或![]() .
.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
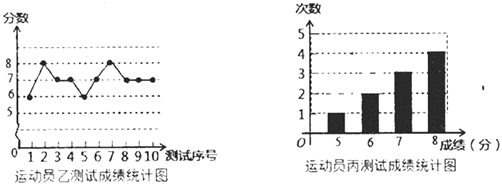
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?