Question

【题目】阅读材料，回答问题：

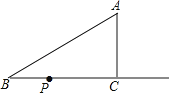
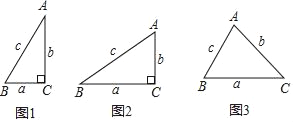
小聪学完了“锐角三角函数”的相关知识后，通过研究发现：如图1，在Rt△ABC中，如果∠C=90°，∠=30°，BC═a=1，AC=b=，AB=c=2，那么==2．通过上网查阅资料，他又知“sin90°=1”，因此他得到“在含30°角的直角三角形中，存在着==的关系．

这个关系对于一般三角形还适用吗？为此他做了如下的探究：

（1）如图2，在R△ABC中，∠C=90°，BC=a，AC=b，AB=C，请判断此时“==”的关系是否成立？答：　 　

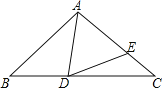
（2）完成上述探究后，他又想“对于任意的锐角△ABC，上述关系还成立吗？”因此他又继续进行了如下的探究：

如图3，在锐角△ABC中，BC=a，AC=b，AB=c，请判断此时“ ==”的关系是否成立？并证明你的判断．（提示：过点C作CD⊥AB于D，过点A作AH⊥BC，再结合定义或其它方法证明）．

Answer 1

【答案】（1）成立；（2）见解析

【解析】

（1）因为=c，=c，=c，推出“==”成立，

（2）作CD⊥AB于D．在Rt△ADC和Rt△BDC中，∠ADC=∠BDC=90°，可得sinA=，sinB=，推出=，=，可得=，同理，作AH⊥BC于H，可证=，即可解决问题.

（1）∵=c， =c， =c，

∴“==”成立，

故答案为成立．

（2）作CD⊥AB于D．

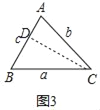
∵在Rt△ADC和Rt△BDC中，∠ADC=∠BDC=90°，

∴sinA=，sinB=，

∴=，=，

∴=，

同理，作AH⊥BC于H，可证=，

∴==．