题目内容
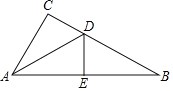
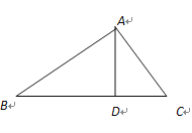
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于E,F两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明:AE=AF.
【答案】(1)见解析;(2)证明见解析.
【解析】
(1)利用基本作图(作已知角的角平分线)作BF平分∠ABC即可;
(2)分析题意,首先根据角平分线的作法作出∠ABC的角平分线,并标注点E、F即可;根据直角三角形的性质,可得出∠BED+∠EBD=90°,∠AFE+∠ABF=90°,进而得出∠BED=∠AFE; 接下来根据对顶角相等,可得出∠AEF=∠AFE,据此可得到结论.
解:(1)如图所示,射线BF即为所求
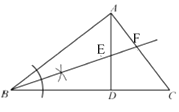
(2)证明:∵AD⊥BC
∴∠ADB=90°
∴∠BED+∠EBD=90°
∵∠BAC=90°
∴∠AFE+∠ABF=90°
∵∠EBD=∠ABF
∴∠AFE=∠BED,
∵∠AEF=∠BED
∴∠AEF=∠AFE
∴AE=AF

练习册系列答案
相关题目
【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
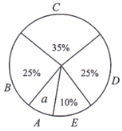
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.