题目内容
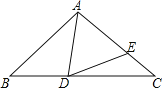
【题目】如图，
是
的内切圆，点
、
分别为
，
上的点，且
为的切线，若的周长为
，
边的长为
．则
的周长为（ ）
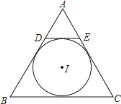
A. 15 B. 7.5 C. 10 D. 9
【答案】C
【解析】
根据切线长定理可以证得：BF+CH=BG+CG=BC，DE=DR+ER=DF+EH，根据△ADE的周长=AD+AE+DE=AD+AE+DF+EH=AF+AH=△ABC的周长-（BF+CH）=△ABC的周长-BC即可求解.
解：∵⊙I是△ABC的内切圆，设与AB，BC，AC的切点分别为：F，G，H，
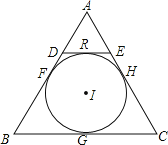
∴BF=BG，CG=CH，DR=DF，ER=EH,
∴BF+CH=BG+CG=BC=5，
DE=DR+ER=DF+EH，
∴△ADE的周长=AD+AE+DE=AD+AE+DF+EH=AF+AH=△ABC的周长-BC-（BF+CH）=△ABC的周长-2BC=20-2×5=10．
故选：C.
练习册系列答案
相关题目
