题目内容
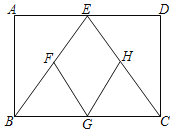
【题目】在四边形ABCD中,BC=CD,连接AC、BD,∠ADB=90°.
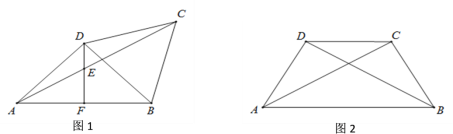
(1)如图1,若AD=BD=BC,过点D作DF⊥AB于点F,交AC于点E:
①∠DAC= °;
②求证:EC=EA+ED;
(2)如图2,若AC=BD,求∠DAC的度数.
【答案】(1)①15°;②见解析;(2)∠DAC=30°.
【解析】
(1)①证明DA=DC,∠ADC=150°,即可求得;②结论:EC=ED+EA.如图1中,设AC交BD于点O,连接BE,在EC上截取EH=EB,由△EBD≌△HBC(SAS),推出DE=CH,可得EC=EH+CH=EB+ED=EA+ED解决问题;
(2)如图2中,作CK⊥BD于K,CH⊥AD交AD的延长线于H,首先证明四边形DHCK是矩形,再证明CH=AC,即可解决问题;
(1)①如图1中,
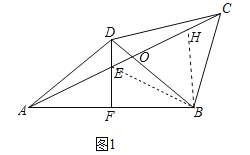
∵AD=BD=BC,BC=CD,
∴BD=BC=CD,
∴△BDC是等边三角形,
∴∠CDB=60°,
∵∠ADB=90°,
∴∠ADC=90°+60°=150°,
∵DA=DC,
∴∠DAC=∠DCA=15°;
故答案为:15°;
②结论:EC=ED+EA.如图1中,设AC交BD于点O,连接BE,在EC上截取EH=EB.

∵DA=DB,DF⊥AB,
∴AF=FB,
∴EA=EB,
∴∠DAF=∠DBF,∠EAB=∠EBA,
∴∠DAE=∠DBE,
∵∠DAE=∠DCO,
∴∠DCO=∠OBE,
∵∠DOC=∠EOB,
∴∠BEO=∠ODC=60°,
∵EH=EB,
∴△EBH是等边三角形,
∴∠EBH=∠DBC=60°,BE=BH,
∴∠EBD=∠HBC,
∵BD=BC,
∴△EBD≌△HBC(SAS),
∴DE=CH,
∴EC=EH+CH=EB+ED=EA+ED.
(2)如图2中,作CK⊥BD于K,CH⊥AD交AD的延长线于H.
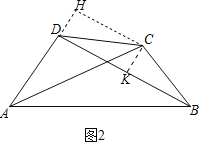
∵∠H=∠CKD=∠HDK=90°,
∴四边形DHCK是矩形,
∴DK=CH,
∵CD=CB.CK⊥BD,
∴DK=![]() BD,
BD,
∵AC=BD,
∴CH=![]() AC,
AC,
在Rt△ACH中,sin∠CAD=![]() ,
,
∴∠CAD=30°.

【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
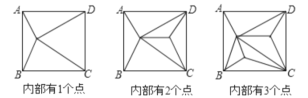
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.