题目内容
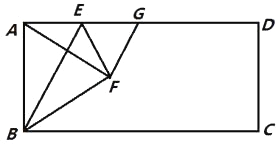
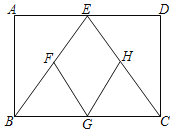
【题目】如图,已知四边形ABCD是矩形,点E,G分别是AD,BC边的中点,连接BE,CE,点F,H分别是BE,CE的中点连接FG,HG.
(1)求证:四边形EFGH是菱形;
(2)当![]() = 时,四边形EFGH是正方形.
= 时,四边形EFGH是正方形.
【答案】(1)见解析;(2)![]()
【解析】
(1)先连接EG,根据四边形ABGE、四边形GCDE都是矩形,得出EF=FG,EH=GH,再根据四边形EFGH是平行四边形,得出FG=EH,最后得到EF=FG=GH=EH,即可得出结论;
(2)根据有一个角是直角的菱形是正方形进行判断即可.
解:(1)连接EG,
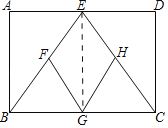
∵矩形ABCD中,AD=BC,E,G分别是AD,BC的中点,
∴AE=BG,
又∵AE∥BG,∠A=90°,
∴四边形ABGE是矩形,
∴∠BGE=90°,
∵F是BE的中点,
∴Rt△BEG中,EF=![]() BE=GF,①
BE=GF,①
同理可得,EH=![]() CE=GH,②
CE=GH,②
∵EG⊥BC,BG=GC,
∴BE=EC,
∴EF=EH,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形;
(2)当AB边和AD边之间满足条件:AD=2AB时,四边形EFGH是正方形.
理由:当AB边和AD边之间满足AD=2AB时,四边形ABGE与四边形EGCD都是正方形,
故∠FGE=∠EGH=45°,
∴∠FGH=90°,
∴菱形EFGH是正方形.
故答案为:![]() .
.

练习册系列答案
相关题目