��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��x2+bx+c��x����A��B���㣬��y���ڵ�C��ֱ��y��x��3����B��C���㣮
��1���������ߵĽ���ʽ��
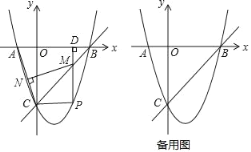
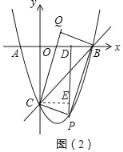
��2����P�ǵ����������������ϵĶ��㣬����P��PD��x���ڵ�D����ֱ��BC�ڵ�M������AC������M��MN��AC�ڵ�N�����P�ĺ�����Ϊt��
�����߶�MN�ij�d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
�ڵ�Q��ƽ����һ�㣬�Ƿ����һ��P��ʹ��B��C��P��QΪ������ı���Ϊ���Σ������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y��x2��2x��3����2����![]() ���ڴ��ڣ�t��1��
���ڴ��ڣ�t��1��![]() ��
��
��������
��1�����������B��C�����꣬Ȼ�����ô���ϵ������������ߵĽ���ʽ��
��2��������S��ABC��S��AMC+S��AMB���������������ʽ����y��m֮��ĺ�����ϵʽ��
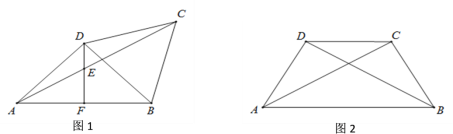
���������ߵĽ���ʽ���ɶ���ʽ����ö������꣬����C��CE��PD�ڵ�E��������������ۣ���ͼ1����BCΪ���εı�ʱ�����ݾ��ε����ʵõ�P��t����3��t�������������ߵĽ���ʽ�����t��1����ͼ2����BCΪ���εĶԽ���ʱ��֤����CPE�ס�PBD���ó�CEBD��PEPD����CE��t��BD��3��t��PD����t2+2t+3������t+1����t��3����PE��PD��DE����t2+2t��3����t2+2t����t��t��2�����г�t��3��t����t��t��2����t+1����t��3������ü��ɣ�
��1����ֱ��y��x��3��B��C���㣬��B��3��0����C��0����3����
����B��3��0����C��0����3������y��x2+bx+c��
��![]()
���![]()
�������ߵĽ���ʽΪy��x2��2x��3��
��2���ٶ���y��x2��2x��3��
��y��0ʱ��x2��2x��3��0��
���x1����1��x2��3��
��A����1��0��
��OA��1��
��OB��OC��3��
���OBC����BCO��45����AC��![]() ��AB��4��
��AB��4��
����AM��
��PD��x���ڵ�D��
���DMB����GBM��45����
�֡ߵ�P�ĺ�����Ϊt��
��DM��DB��3��t��
��S��ABC��S��AMC+S��AMB��
��![]()
��![]()
��![]()
�ڴ��ڣ�t��1��![]() ��
��
��y��x2��2x��3����x��1��2��4��
�������ߵĶ�������Ϊ��1����4����
����C��CE��PD�ڵ�E��
��ͼ��1������BCΪ���εı�ʱ��
�ɡ�BCP��90������BCE��45�����ɵá�EPC����ECP��45����
��PE��CE��t��
��P��t����3��t����
��P��t����3��t������y��x2��2x��3��
�é�3��t��t2��2t��3��
���t1��0���������⣬��ȥ����t2��1��
��ͼ��2������BCΪ���εĶԽ���ʱ��
�ߡ�PCE+��CPE��90������CPE+��BPD��90����
���PCE����BPD��
���CPE�ס�PBD��
��![]() ����CEBD��PEPD��
����CEBD��PEPD��
�ߵ�P�ĺ�����Ϊt��
��CE��t��BD��3��t��PD����t2+2t+3������t+1����t��3����PE��PD��DE����t2+2t��3����t2+2t����t��t��2����
��t��3��t����t��t��2����t+1����t��3����
��������t2��t��1��0��
���![]() ���������⣬��ȥ����
���������⣬��ȥ����
���Ͽ�֪��t��ֵΪ1��![]() ��
��

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�