题目内容
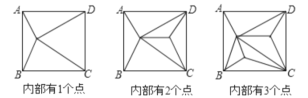
【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
【答案】(1)8,10,2n+2;(2)原正方形不能被分割成2021个三角形,理由见详解.
【解析】
(1)由图形中三角形的个数,观察发现,每多一个点,三角形的个数增加2,然后据此规律填表即可;
(2)根据(1)中规律,列式求解,如果n是整数,则能分割,如果不是整数,则不能分割.
(1)有1个点时,内部分割成4个三角形;
有2个点时,内部分割成4+2=6个三角形;
有3个点时,内部分割成4+2×2=8个三角形;
有4个点时,内部分割成4+2×3=10个三角形;
…
以此类推,有n个点时,内部分割成4+2×(n1)=(2n+2)个三角形,
填表如下:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | ___8__ | ___10__ | ... | ____2n+2_ |
故答案是:8,10,2n+2;
(2)不能,理由如下:
理由如下:由(1)知2n+2=2021,
解得:n=1009.5,不是整数,不符合题意,
∴原正方形不能被分割成2021个三角形.

【题目】随着人们的生活水平的提高,家用轿车越来越多地进入家庭.小明家买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣9 | ﹣13 | 0 | ﹣14 | ﹣16 | +33 | +19 |
(1)求出这7天的行驶路程中最多的一天比最少的一天多行驶多少千米?
(2)若每行驶100km需用汽油8升,每升汽油6.5元,计算小明家这7天的汽油费用共是多少元?