题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,将
上,将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,且
处,且![]() .
.
(1)求![]() 的长;
的长;
(2)点![]() 是射线
是射线![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,
,![]() ,
,![]() 的面积与
的面积与![]() 的面积相等,
的面积相等,
①当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的长;
的长;
②当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ________;
________;
(3)将直线![]() 平移,平移后的直线与直线
平移,平移后的直线与直线![]() ,直线
,直线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,以线段
,以线段![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 与点
与点![]() 在直线
在直线![]() 两侧,连接
两侧,连接![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3)![]() .
.
【解析】
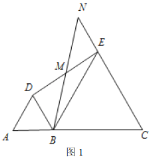
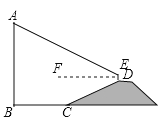
(1)如图1中,连接DF,在Rt△DCF中,利用勾股定理,构建方程即可解决问题.
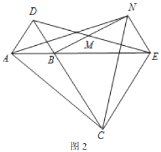
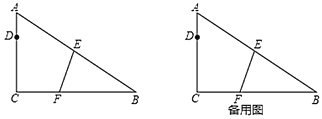
(2)①如图2-1中,当DG∥BC时,S△DGC=S△DGB.设BG=x.利用平行线分线段成比例定理即可解决问题.
②如图2-2中,当点G在BA的延长线上时,证明AB=2AG时,满足条件.
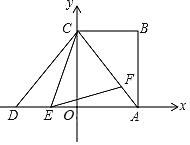
(3)如图3中,当PD∥BC时,作QK⊥BC于K.利用全等三角形以及相似三角形的性质解决问题即可.
解:(1)如图1中,连接DF,
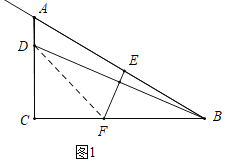
∵将△ABC沿直线EF折叠,点B恰好落在AC边上的点D处
∴DF=BF
在Rt△DCF中,DF2=DC2+CF2,
∴(6-CF)2=9+CF2,
∴CF=![]() .
.
(2)①如图2-1中,当DG∥BC时,S△DGC=S△DGB.设BG=x.

在Rt△ACB中,AC=4,BC=6,
∴AB=![]() ,
,
∵DG∥BC,
∴![]() ,
,
∴![]() ,
,
∴x=![]() .
.
②如图2-2中,当点G在BA的延长线上时,
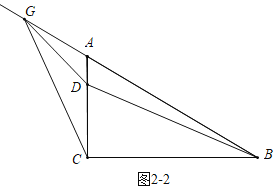
∵CD=3AD,
∴S△GDC=3S△GAD,
∴当S△ADB=2S△ADG时,S△GDC=S△GBD,
∴AB=2AG,
∴AG=![]() ,
,
∴GB=3![]() .
.
综上:GB=![]() 或
或![]() ;
;
(3)如图3中,当PD∥BC时,作QK⊥BC于K.

∵四边形MNPQ是正方形,
∴易证△PDN≌△NCM≌△MKA,
∴KQ=CM=DN,KM=CN=PD,
∵△PDN∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴PD=2DN,
∴CN=2DN,
∴DN=1,CN=2,
∴KQ=DN=CM=1,KM=CN=2,
∴BK=9,
∴tan∠QBC=![]() .
.

 名校课堂系列答案
名校课堂系列答案