��Ŀ����
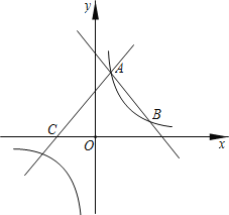
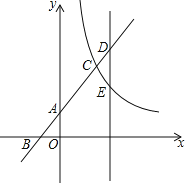
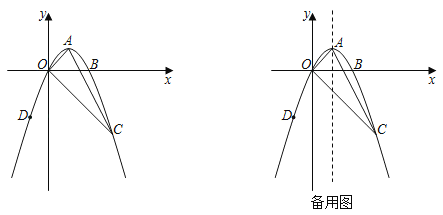
����Ŀ����֪������y��ax2+bx+c��x�ύ��O��B���㣬�䶥��A����Ϊ��1��1������CΪ�������ڵ��������ڵ�һ�㣬������Ϊ��3����3����
��1���������߽���ʽ��
��2����DΪ�������ڵ��������ڵ�һ�㣬����D��x�������߶Σ�����ΪH���Ƿ���ڵ�Dʹ�á�DHO���AOC���ƣ�������ڣ��������D���꣬��������ڣ���˵�����ɣ�
��3����E��F�ֱ�Ϊ�������Լ������߶Գ����ϵ������㣬�����Ƿ������BOΪ�ߣ�B��O��E��FΪ�����ƽ���ı��Σ����������ֱ��д����E���꣬�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+2x����2�����ڣ�D����1����3������3�����ڣ���E������Ϊ����1����3����3����3����
��������
��1���������������ʽ����ʽy��a��x��1��2+1���ٽ���C���뼴�ɣ�
��2�����D������Ϊ��m����m2+2m������DH��x�ᣬ��ֱΪH������OD���ֱ����AO��![]() ��OC��3
��OC��3![]() �������������
�������������![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����HO����m��HD��m2��2m���ɵ�
����HO����m��HD��m2��2m���ɵ�![]() ��
��![]() ����ü��ɣ���
����ü��ɣ���![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����HO����m��HD��m2��2m���ɵ�
����HO����m��HD��m2��2m���ɵ�![]() ��
��![]() ����ü��ɣ�
����ü��ɣ�
��3�����E��a����a2+2a������F��1����a2+2a�����ٵ�OEFBΪƽ���ı���ʱ��OB��EF������1��a��2����E����1����3�����ڵ�OFEBΪƽ���ı���ʱ��OB��FE������a��1��2�����ɵó���E�����꣮
�⣺��1����������������ߵĽ���ʽΪy��a��x��1��2+1��
�������߾�����C��3����3����
�ੁ3��a��3��1��2+1��
��a����1��
��y����x2+2x��
��2�����D������Ϊ��m����m2+2m������DH��x�ᣬ��ֱΪH������OD��
��A��1��1����C��3����3����
���A��C�ֱ���һ��������ƽ���������������ƽ�����ϣ�
���AOC��90����
��AO��![]() ��OC��3
��OC��3![]() ��
��
����DHO����AOC���ƣ�
�ߡ�DHO����AOC��90����
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��HO����m��HD��m2��2m��
��![]() ��
��![]() ��
��
���m����1��m��0���ᣩ��
��D����1��3����
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��HO����m��HD��m2��2m��
��![]() ��
��![]() ��
��
���m��![]() ���ᣩ��m��0���ᣩ��
���ᣩ��m��0���ᣩ��
����������D����1����3����
��3�����ڣ���E������Ϊ����1����3����3����3����
�������£���BOΪ�ߣ�B��O��E��FΪ�����ƽ���ı��Σ�
��OB��EF��OB��EF��2��
���E��a����a2+2a������F��1����a2+2a����
�ٵ�OEFBΪƽ���ı���ʱ��OB��EF��
��1��a��2��
��a����1��
��E����1����3����
�ڵ�OFEBΪƽ���ı���ʱ��OB��FE��
��a��1��2��
��a��3��
��E��3����3����
����������������BOΪ�ߣ�B��O��E��FΪ�����ƽ���ı��Σ���E������Ϊ����1����3����3����3����

����Ŀ����֪���κ���![]() �е�
�е�![]() ��
��![]() �����±�
�����±�
| �� |
| 0 | 1 | 2 | 3 | �� |
| �� | 0 |
|
|
|
| �� |
��l��![]() ________��
________��![]() ________��
________��
��2������ͼ��Գ�����____________��
��3�������![]() ��
��![]() ��ͼ���ϵ㣬��
��ͼ���ϵ㣬��![]() ________��
________��
��4������ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() �����
�����![]() ����Ϊ________��
����Ϊ________��