题目内容
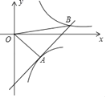
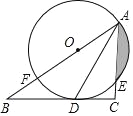
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
【答案】(1)证明见解析 (2)![]()
【解析】
(1)连接OD,只要证明OD∥AC即可解决问题;
(2)连接OE,OE交AD于K.只要证明△AOE是等边三角形即可解决问题.
(1)连接OD.
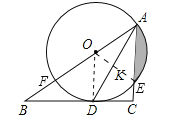
∵OA=OD,∴∠OAD=∠ODA.
∵∠OAD=∠DAC,∴∠ODA=∠DAC,∴OD∥AC,∴∠ODB=∠C=90°,∴OD⊥BC,∴BC是⊙O的切线.
(2)连接OE,OE交AD于K.
∵![]() ,∴OE⊥AD.
,∴OE⊥AD.
∵∠OAK=∠EAK,AK=AK,∠AKO=∠AKE=90°,∴△AKO≌△AKE,∴AO=AE=OE,∴△AOE是等边三角形,∴∠AOE=60°,∴S阴=S扇形OAE﹣S△AOE![]() 22
22![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目