Question

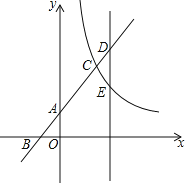
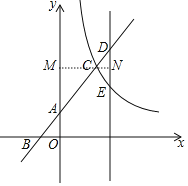
【题目】如图所示，直线y＝x+2与坐标轴交于A、B两点，与反比例函数y＝（x＞0）交于点C，已知AC＝2AB．

（1）求反比例函数解析式；

（2）若在点C的右侧有一平行于y轴的直线，分别交一次函数图象与反比例函数图象于D、E两点，若CD＝CE，求点D坐标．

Answer 1

【答案】（1）y＝；（2）D（6，8）．

【解析】

（1）作CM⊥y轴于M，如图，利用直线解析式确定A（0，2），B（﹣2，0），再根据平行线分线段成比例定理求出MC＝4，AM＝4，则C（4，6），然后把C点坐标代入y＝中求出k得到反比例函数解析式；

（2）MC交直线DE于N，如图，证明△CND为等腰直角三角形得到CN＝DN，再利用CD＝CE得到CN＝NE＝DN，设CN＝t，则N（4+t，6），D（4+t，6+t），E（4+t，6﹣t），然后把E（4+t，6﹣t）代入y＝得（4+t）（6﹣t）＝24，最后解方程求出t得到D点坐标．

解：（1）作CM⊥y轴于M，如图，

当x＝0时，y＝x+2＝2，则A（0，2），

当y＝0时，x+2＝0，解得x＝﹣2，则B（﹣2，0），

∵MC∥OB，

∴＝＝＝2，

∴MC＝2OB＝4，AM＝2OA＝4，

∴C（4，6），

把C（4，6）代入y＝得k＝4×6＝24，

∴反比例函数解析式为y＝；

（2）MC交直线DE于N，如图，

∵MC＝MA，

∴△MAC为等腰直角三角形，

∴∠ACM＝45°，

∴∠DCN＝45°，

∴△CND为等腰直角三角形，

∴CN＝DN，

∵CD＝CE，

∴CN＝NE＝DN，

设CN＝t，则N（4+t，6），D（4+t，6+t），E（4+t，6﹣t），

把E（4+t，6﹣t）代入y＝得（4+t）（6﹣t）＝24，解得t1＝0（舍去），t2＝2，

∴D（6，8）．