题目内容
【题目】如图,直线y1=-x+4与双曲线y=![]() (k≠0)交于A、B两点,点A的坐标为(1,m),经过点A的直线y2=x+b与x轴交于点C.
(k≠0)交于A、B两点,点A的坐标为(1,m),经过点A的直线y2=x+b与x轴交于点C.
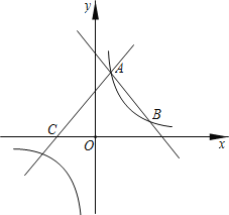
(1)求反比例函数的表达式以及点C的坐标;
(2)点P是x轴上一动点,连接AP,若△ACP是△AOB的面积的一半,求此时点P的坐标.
【答案】(1)y=![]() ,C(-2,0);(2)P点为(-
,C(-2,0);(2)P点为(-![]() ,0)或(-
,0)或(-![]() ,0).
,0).
【解析】
(1)把A(1,m)代入y1=-x+4中,求出m的值,即可求出点A的坐标,从而求出反比例函数的解析式和直线AC的解析式,联立反比例和BC直线解析式,即可求出点C的坐标;
(2)连接OA、OB,分别作AM⊥x轴于M,BN⊥x轴于N,求出△AOB的面积,设P(x,0),根据△ACP是△AOB的面积的一半,列出方程求出x,即可求出P点坐标.
(1)把A(1,m)代入y1=-x+4得,m=-1+4=3,
∴A(1,3),
∵点A在双曲线y=![]() (k≠0)上,
(k≠0)上,
∴k=1×3=3,
∴反比例函数的表达式为y=![]() ,
,
∵直线y2=x+b经过点A,
∴b=2,
∴直线y2=x+2,
令y2=0,求得x=-2,
∴C(-2,0);
(2)连接OA、OB,分别作AM⊥x轴于M,BN⊥x轴于N,
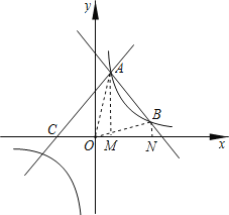
由题意得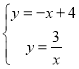 ,
,
解得![]() 或
或![]() ,
,
∴A(1,3),B(3,1),
∴AM=3,BN=1,MN=2,
∴S△AOB=S△AOM+S梯形AMNB-S△BON=S梯形AMNB=![]() =4,
=4,
设P(x,0),
∴CP=|x+2|,
∴S△ACP=![]() =
=![]() S△AOB,
S△AOB,
∴|x+2|=![]() ,则x=±
,则x=±![]() -2,
-2,
∴x=-![]() 或-
或-![]()
∴P点为(-![]() ,0)或(-
,0)或(-![]() ,0).
,0).

【题目】某车间准备采取每月任务定额,超产有奖的措施提高工作效率,为制定一个恰当的生产定额,从该车间200名工人中随机抽取20人统计其某月产量如下:
每人生产零件数 | 260 | 270 | 280 | 290 | 300 | 310 | 350 | 520 |
人 数 | 1 | 1 | 5 | 4 | 3 | 4 | 1 | 1 |
(1)请应用所学的统计知识.为制定生产定额的管理者提供有用的参考数据;
(2)你认为管理者将每月每人的生产定额定为多少最合适?为什么?
(3)估计该车间全年可生产零件多少个?