��Ŀ����
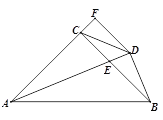
����Ŀ����ͼ1��������ȫ�ȵ�ֱ��������ֽƬ��ABC�͡�DEF������һ�����С�ACB����E��90�㣬BC��DE��6��AC��FE��8������D���AB���е��غϣ�
��1����DE������C��DF��AC�ڵ�G�����ص����֣���DCG���������
��2��������������ϣ����С�������⣨1��������������DEF�Ƶ�D��ת��ʹDE��AB��AC�ڵ�H��DF��AC�ڵ�G����ͼ2�����ص����֣���DGH���������
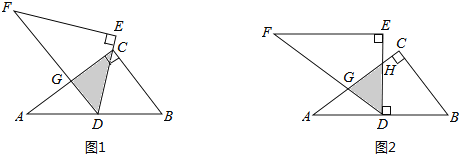
���𰸡�6�� ![]() ��
��
�����������������(1)����������ó���ABC����FDEȫ�ȣ��Ӷ��ó�CG��DG�Ĵ�С��Ȼ����������ε�������㷨����������ε������(2)����������ó���ABC����FDEȫ�ȣ�����Rt��ABC�Ĺ��ɶ������AB�ij��ȣ������е�ó�AD�ij��ȡ�����BH������Rt��ADH�Ĺ��ɶ������DH�ij��ȣ��Ӷ��ó���DGH�����.
���������(1)���ߡ�ACB=90����D��AB���е㣬��DC=DB=DA�����B=��DCB�����ߡ�ABC�ա�FDE��
���FDE=��B�����FDE=��DCB����DG��BC�����AGD=��ACB=90������DG��AC������DC=DA��
��G��AC���е㣮��![]() ����
����![]()
(2)����ͼ2��ʾ���ߡ�ABC�ա�FDE�����B=��1���ߡ�C=90����ED��AB�����A+��B=90������A+��2=90����
���B=��2�����1=��2����GH=GD���ߡ�A+��2=90������1+��3=90�������A=��3����AG=GD��
��AG=GH������GΪAH���е㣻 ��Rt��ABC�У�![]() ��
��
��D��AB�е㣬��![]() ��
��
����BH����DH��ֱƽ��AB����AB=BH����AH=x����BH=x��CH=8-x��
�ɹ��ɶ����ã���8-x��2+62=x2�����x=�� ��DH=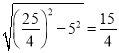 ��
��
��S��DGH��S��ADH=������5����

 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�