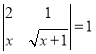Question

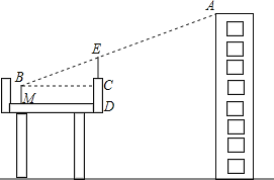
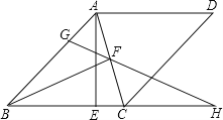
【题目】 菱形ABCD中，F是对角线AC的中点，过点A作AE⊥BC垂足为E，G为线段AB上一点，连接GF并延长交直线BC于点H．

（1）当∠CAE=30°时，且CE=，求菱形的面积；

（2）当∠BGF+∠BCF=180°，AE=BE时，求证：BF=(+1)GF．

Answer 1

【答案】（1）6；（2）证明见解析．

【解析】

（1）只要证明△ABC是等边三角形，即可解决问题；

（2）如图，连接GC，作GM⊥GF交BF于M．证明△BGC是等腰直角三角形，再证明△BGM≌△CGF即可解决问题；

（1）∵四边形ABCD是菱形，

∴AB=BC，

∵AE⊥BC，∠EAC=30°，

∴∠ACE=60°，AC=2EC=2，

∴△ABC，△ACD都是等边三角形，

∴S菱形ABCD=2S△ABC=2××(2)2=6．

（2）如图，连接GC，作GM⊥GF交BF于M．

∵四边形ABCD是菱形，

∴BA=BC，∵AF=FC，

∴BF⊥AC，

∴∠BFA=90°，

∵∠BGF+∠BCF=180°，∠AGF+∠BGF=180°，

∴∠AGF=∠ACB，∵∠GAF=∠CAB

∴△AGF∽△ACB，

∴=，

∴=，∵∠CAG=∠BAF，

∴△CAG∽△BAF，

∴∠CGA=∠BFA=90°，

∵AE⊥BE，AE=BE，

∴∠ABE=45°，

∴∠GBC=∠GCB=45°，

∴GB=GC，

∵∠BGC=∠MGF，

∴∠BGM=∠CGF，

∵∠GBM=∠GCF，

∴△BGM≌△CGF，

∴BM=CF，GM=GF，FM=GF，

∵∠AGC=90°AF=FC，

∴GF=FC=BM，

∴BF=BM+FM=GF+GF=(+1)GF．