题目内容
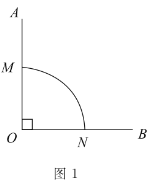
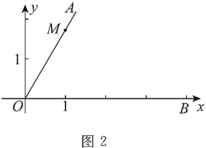
【题目】在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图2中阴影部分的周长与图1中阴影部分的周长的差为l,若要知道l的值,只要测量图中哪条线段的长( )
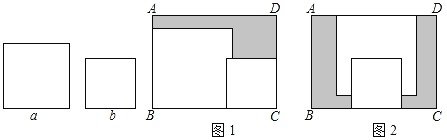
A.aB.bC.ADD.AB
【答案】D
【解析】
根据周长的定义,列出算式l=2AD+4AB﹣2b﹣(2AD+2AB﹣2b),再去括号,合并同类项即可求解.
解:图1中阴影部分的周长=2AD+2AB﹣2b,
图2中阴影部分的周长=2AD﹣2b+4AB,
l=2AD+4AB﹣2b﹣(2AD+2AB﹣2b)=2AD+4AB﹣2b﹣2AD﹣2AB+2b=2AB.
故若要知道l的值,只要测量图中线段AB的长.
故选:D.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
【题目】有这样一个问题:探究函数![]() 的图象与性质并解决问题.
的图象与性质并解决问题.
小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)取几组![]() 与
与![]() 的对应值,填写在下表中.
的对应值,填写在下表中.
| … |
|
|
| 0 | 1 | 1.2 | 1.25 | 2.75 | 2.8 | 3 | 4 | 5 | 6 | 8 | … |
| … | 1 | td style="width:6%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.62pt; vertical-align:middle">2 | 3 | 6 | 7.5 | 8 | 8 | 7.5 | 6 | 3 |
| 1.5 | 1 | … |
![]() 的值为_____________;
的值为_____________;
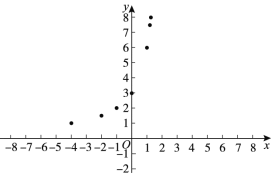
(3)如下图,在平面直角坐标系![]() 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数![]() 的图象是轴对称图形,它的对称轴是____________;
的图象是轴对称图形,它的对称轴是____________;
②过点![]() 作直线
作直线![]() 轴,与函数
轴,与函数![]() 的图象交于点
的图象交于点![]() (点
(点![]() 在点
在点![]() 的左侧),则
的左侧),则![]() 的值为____________.
的值为____________.