题目内容
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.
(1)求A、B两种型号汽车的进货单价;
(2)销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
【答案】(1)A、B两种型号汽车的进货单价为:10万元、8万元;(2)A、B两种型号的汽车售价各为14万元、12万元时,每周销售这两种汽车的总利润最大,最大利润是32万元..
【解析】
(1)由题意根据购进两种型号的汽车数量相同列出分式方程即可求解;
(2)由题意根据销售利润等于每台汽车的利润乘以销售量列出二次函数关系即可求解.
解:(1)设B型汽车的进货单价为x万元,根据题意得![]() =
=![]() ,解得x=8,
,解得x=8,
经检验x=8是原分式方程的根.
答:A、B两种型号汽车的进货单价为:10万元、8万元.
(2)设两种汽车的总利润为w万元,根据题意得
w=(x+2﹣10)[﹣(x+2)+18]+(x﹣8)(﹣x+14)
=﹣2x2+48x﹣256
=﹣2(x﹣12)2+32
∵﹣2<0,当x=12时,w有最大值为32.
答:A、B两种型号的汽车售价各为14万元、12万元时,每周销售这两种汽车的总利润最大,最大利润是32万元.

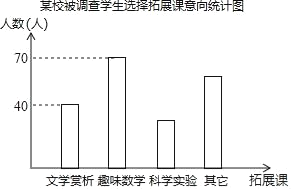
【题目】为丰富学生的课余生活,某校记划开展三种拓展课活动,分别是“文学赏析”,“趣味数学”,“科学实验”等项目,要求每位学生自主选择其中一项拓展课参加.随机抽取该校各年段部分学生,对选择拓展课的意向进行调査,将调查的结果制作成以下统计图和不完整的统计表.
某校被调查学生选择拓展课意向统计表
选择意向 | 所占百分比 |
文学赏析 |
|
趣味数学 | 35% |
科学实验 |
|
其它 | 30% |
(1)该校有2000名学生,请你估计大约有多少名学生参加科学实验拓展课,并补全统计表.
(2)该校参加科学实验拓展课的学生随机分成A,B,C三个人数相同的班级.小慧和小明都参加科学实验拓展课,求他们同班级的概率(画树状图或列表法求解)