题目内容
【题目】某校举办球赛,分为若干组,其中第一组有A,B,C,D,E五个队.这五个队要进行单循环赛,即每两个队之间要进行一场比赛,每场比赛采用三局两胜制,即三局中胜两局就获胜.每场比赛胜负双方根据比分会获得相应的积分,积分均为正整数.这五个队完成所有比赛后得到如下的积分表.
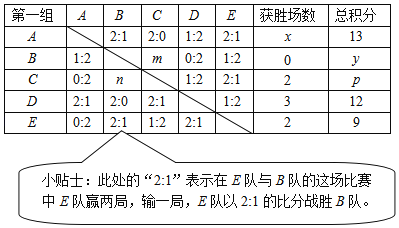
根据上表回答下列问题:
(1)第一组一共进行了 场比赛,A队的获胜场数x为 ;
(2)当B队的总积分y=6时,上表中m处应填 ,n处应填 ;
(3)写出C队总积分p的所有可能值为: .
【答案】(1)10,3;(2)0:2, 2:0;(3)9或10
【解析】
(1)按照5个队中每个队都要和另外4个队进行一场比赛,而A与B和B与A属于同一场比赛,列式计算或直接从表中数一下即可得比赛场数;根据表中比赛结果可直接得出A队的获胜场数x的值;
(2)每场比赛的结果有四种:0:2,1:2,2:1,2:0,设以上四种得分为a,b,c,d,且a<b<c<d,根据E和A的总分可得关于a,b,c,d的等式,化简即可得出a,b,c,d的值,设m对应的积分为x,根据题意得关于x的方程,解得x的值,则可得答案;
(3)C队胜2场,分两种情况:当C、B的结果为2:0时;当C、B的结果为2:1时,分别计算出p的值即可.
解:(1)∵![]() (场),
(场),
∴第一组一共进行了10场比赛;
∵每场比赛采用三局两胜制,A、B的结果为2:1,A、C的结果为2:0,A、E的结果为2:0,
∴A队的获胜场数x为3;
故答案为:10,3;
(2)由题可知:每场比赛的结果有四种:0:2,1:2,2:1,2:0,
根据题意可知每种结果都会得到一个正整数积分,设以上四种得分为a,b,c,d,且a<b<c<d,
根据E的总分可得:a+c+b+c=9,
∴a=1,b=2,c=3,
根据A的总分可得:c+d+b+d=13,
∴d=4,
设m对应的积分为x,
当y=6时,b+x+a+b=6,即2+x+1+2=6,
∴x=1,
∴m处应填0:2;
∴B:C=0:2,
∴C:B=2:0,
∴n处应填2:0;
(3)∵C队胜2场,
∴分两种情况:当C、B的结果为2:0时,
p=1+4+3+2=10;
当C、B的结果为2:1时,
p=1+3+3+2=9;
∴C队总积分p的所有可能值为9或10.
故答案为:9或10.

【题目】改革开放以来,人们的支付方式发生了巨大转变,近年来,移动支付已成为主要的支付方式之一,为了解某校学生上个月![]() 两种移动支付方式的使用情况,从全校
两种移动支付方式的使用情况,从全校![]() 名学生中随机抽取了
名学生中随机抽取了![]() 人,发现样本中
人,发现样本中![]() 两种支付方式都不使用的有
两种支付方式都不使用的有![]() 人,样本中仅使用
人,样本中仅使用![]() 种支付方式和仅使用
种支付方式和仅使用![]() 种支付方式的学生的支付金额
种支付方式的学生的支付金额![]() (元)的分布情况如下:
(元)的分布情况如下:
支付金额 支付方式 |
|
|
|
仅使用 |
|
|
|
仅使用 |
|
|
|
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生使用A支付方式的概率大于他使用B支付方式的概率;
②根据样本数据估计,全校1000名学生中.同时使用A、B两种支付方式的大约有400人;
③样本中仅使用A种支付方式的同学,上个月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的同学,上个月的支付金额的平均数一定不低于1000元.其中合理的是( )
A.①③B.②④C.①②③D.①②③④
【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
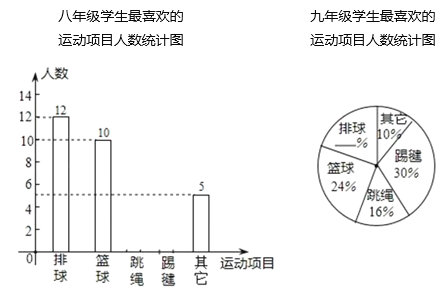
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?