题目内容
【题目】如图,已知二次函数y=﹣x2+bx+c的图象经过点A(3,1),点B(0,4).
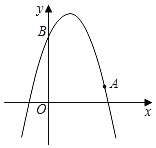
(1)求该二次函数的表达式及顶点坐标;
(2)点C(m,n)在该二次函数图象上.
①当m=﹣1时,求n的值;
②当m≤x≤3时,n最大值为5,最小值为1,请根据图象直接写出m的取值范围.
【答案】(1)y=﹣(x﹣1)2+5,顶点为(1,5);(2)①n=1;②﹣1≤m≤1
【解析】
(1)根据待定系数法即可求得;
(2)①把x=﹣1代入(1)中求得的解析式求得函数y的值,即可求得n的值;
②把y=1代入抛物线解析式求得对应的x的值,然后根据图象即可求得m的取值范围.
解:(1)∵二次函数y=﹣x2+bx+c的图象经过点A(3,1),点B(0,4).
∴![]() ,解得
,解得![]() ,
,
∴该二次函数为y=﹣x2+2x+4,
∵y=﹣(x﹣1)2+5,
∴顶点为(1,5);
(2)∵点C(m,n)在该二次函数图象上,
①当m=﹣1时,则C(﹣1,n),
把C(﹣1,n)代入y=﹣x2+2x+4得,
n=-1-2+4=1,
∴n=1;
②∵y=﹣(x﹣1)2+5,
∴当x=3时,y=﹣(3﹣1)2+5=1,抛物线对称轴是直线x=1,函数的最大值是5,
∴点(3,1)关于关于对称轴的对称点是(-1,1),抛物线的顶点为(1,5).
∵当m≤x≤3时,n最大值为5,最小值为1,
∴m的取值范围是-1≤m≤1.

【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
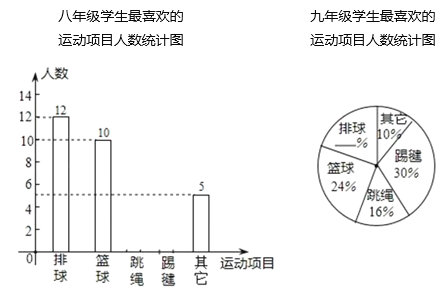
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?