Question

【题目】对于平面直角坐标系xOy中的点P，Q，给出如下定义：若P，Q为某个三角形的顶点，且边PQ上的高h，满足h＝PQ，则称该三角形为点P，Q的“生成三角形”．

（1）已知点A（4，0）；

①若以线段OA为底的某等腰三角形恰好是点O，A的“生成三角形”，求该三角形的腰长；

②若Rt△ABC是点A，B的“生成三角形”，且点B在x轴上，点C在直线y＝2x﹣5上，则点B的坐标为　 　；

（2）⊙T的圆心为点T（2，0），半径为2，点M的坐标为（2，6），N为直线y＝x+4上一点，若存在Rt△MND，是点M，N的“生成三角形”，且边ND与⊙T有公共点，直接写出点N的横坐标的取值范围．

Answer 1

【答案】（1）①；②（1，0），（3，0）或（7，0）；（2）点N的横坐标的取值范围为.

【解析】

（1）①如图（见解析），设满足条件的三角形为等腰，过点R作于点H，由等腰三角形的性质得，再根据“生成三角形”的定义可得，最后利用勾股定理即可得；

②依题意，按点分别为直角顶点三种情况讨论，根据“生成三角形”的定义和直线的解析式分别建立等式，求解即可；

（2）根据点分别为直角顶点三种情况讨论，根据“生成三角形”的定义、结合圆的切线性质列出等式，求解即可.

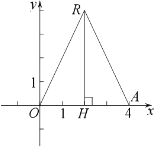
（1）①如图，设满足条件的三角形为等腰，则

过点R作于点H

∵以线段OA为底的等腰恰好是点O，A的“生成三角形”

在中，利用勾股定理得：

故该三角形的腰长为；

②依题意，分以下三种情况讨论：

当A为直角顶点时，则

因点A的坐标为

令代入得，即

设点B的坐标为

则，解得或

故点B的坐标为或

当B为直角顶点时，则

设点B的坐标为，则

令代入得，即

则有

两边平方化简得，解得或

故点B的坐标为或

当C为直角顶点时，如图，过点C作于点D

设点D的坐标为，则

令代入得

由“生成三角形”的定义得

则

又

，即

令，则

化简得，此方程的根的判别式，方程没有实数根

则点C不能为的直角顶点

综上，点B的坐标为，或；

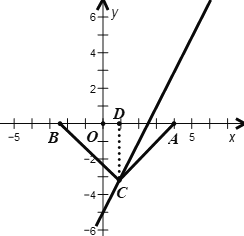
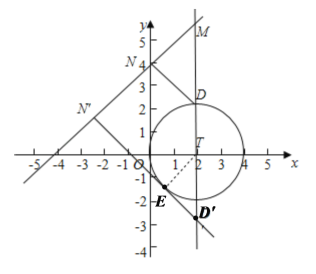
（2）当N为直角顶点时

由点M的坐标可知，点M在直线上

由直线可知，

则当点D在MT所在直线时，是点M，N的“生成三角形”

如图，点N和是符合条件的两个临界位置

由图可知，点D的坐标为，

在中，

设点N的坐标为

由两点之间距离公式得

解得，再代入直线得

当点N在处时，图中也是符合条件的“生成三角形”

此时，恰好与圆T相切，半径

则是等腰直角三角形，且

则点的坐标为，设点的坐标为

由两点之间距离公式得

解得，再代入直线得

故当点N为直角顶点时，点N的横坐标的取值范围为

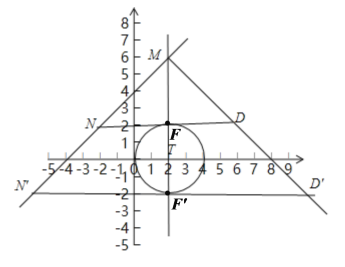
当点M为直角顶点时，

如图，和均平行于x轴，且与圆T分别相切于点F，

由平行线的性质和直线可知，

则和都是等腰直角三角形

因此，和都是符合条件的“生成三角形”， 此时，点N和是符合条件的两个临界位置

设点N的坐标为

点F的坐标为

点N的纵坐标为2，即

将代入得

同理可得

故当点M为直角顶点时，点N的横坐标的取值范围为

当点D为直角顶点时，同（1）②中，当C为直角顶点时的思路一样，可证此时不存在符合条件的

综上，点N的横坐标的取值范围为.