题目内容
【题目】已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
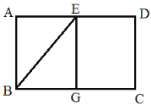
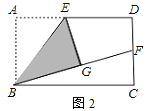
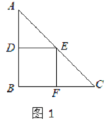
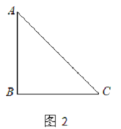
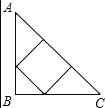
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为![]() ,则
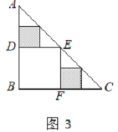
,则![]() =___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为
=___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为![]() ,则
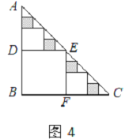
,则![]() =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为
=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为![]() ;按照同样的方法继续操作下去……,第
;按照同样的方法继续操作下去……,第![]() 次裁剪得到_________个新的正方形,它们的面积的和
次裁剪得到_________个新的正方形,它们的面积的和![]() =______________.
=______________.
【答案】(1)画图见解析;(2)(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】(1)利用斜边长的![]() ,向斜边作垂线得出正方形即可;
,向斜边作垂线得出正方形即可;
(2)根据题意,可求得S1,S2,S3,同理可得规律:Sn即是第n次剪取后面积和,根据此规律求解即可答案.
(1)如图所示;
(2)∵四边形DBFE是正方形,
∴DE=EF=BF=DB,∠EFC=∠ADE=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴AD=DE=EF=CF=BF=BD,
∵AB=BC=1,
∴DE=EF=![]() ,
,
∴S正方形DBFE=S1=![]() ×
×![]() =
=![]() ;
;
同理:S2即是第二次剪取后的面积和,
Sn即是第n次剪取后的面积和,
∴第一次剪取后的面积和为:S1=![]() =
=![]() ,
,
第二次剪取后的面积和为:S2=![]() ×
×![]() ×2=
×2=![]() =
=![]() ,
,
第三次剪取后剩余三角形面积和为:S3=![]() ×
×![]() ×4=
×4=![]() =
=![]() ,
,
…
第n次剪取后面积和为:Sn=![]() ×
×![]() ×2n1=
×2n1=![]() .
.
故答案为:![]() ,
,![]() ,2n1,
,2n1,![]() .
.