题目内容
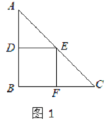
【题目】已知：△ABC中AB=AC，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q.
探究:（1）线段QM、PM、AB之间有什么关系？并说明你的理由.
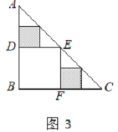
（2）当M位于BC的什么位置时, 四边形AQMP是菱形？并说明你的理由.
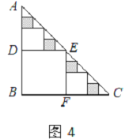
（3）当△ABC满足什么条件菱形AQMP是正方形？
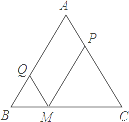
【答案】（1）AB=QM+PM，证明见解析；（2）当M为底边BC的中点时,四边形AQMP为菱形，证明见解析；（3）当∠A＝90°时, 菱形AQMP为正方形.
【解析】（1）根据平行四边形的判定得出平行四边形AQMP，求出BQ＝MQ即可；
（2）求出AQ＝QM，根据菱形的判定推出即可；
（3）根据有一个角是直角的菱形是正方形求解即可.
（1）AB=QM+PM
证明：∵PM‖AB,QM‖AC
∴四边形AQMP为平行四边形
∴PM＝AQ
∵QM‖AC
∴∠C=∠QMB
∵AB=AC
∴∠C=∠B
∴∠B=∠QMB
∴BQ=MQ
∵AB=AQ+BQ
∴AB=QM+PM
（2）当M为底边BC的中点时,四边形AQMP为菱形
证明：连接AM
∵M为底边BC的中点，AB=AC
∴∠BAM＝∠MAC
∵PM‖AB
∴∠BAM＝∠AMP
∴∠MAC＝∠AMP
∴PA＝PM
∴平行四边形AQMP为菱形
(3)当∠A＝90°时, 菱形AQMP为正方形
由（2）知，四边形AQMP为菱形，
∵∠A＝90°，
∴菱形AQMP为正方形.
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
相关题目
