Question

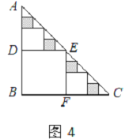
【题目】如图，等边三角形纸片ABC中，点D在边AB（不包含端点A、B）上运动，连接CD，将∠ADC对折，点A落在直线CD上的点A′处，得到折痕DE；将∠BDC对折，点B落在直线CD上的点B′处，得到折痕DF．

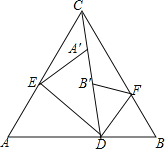
（1）若∠ADC=80°，求∠BDF的度数；

（2）试问∠EDF的大小是否会随着点D的运动而变化？若不变，求出∠EDF的大小；若变化，请说明理由．

Answer 1

【答案】（1）∠BDF=50°；（2）∠EDF=90°．

【解析】

（1）根据翻折的性质解答即可；

（2）利用角平分线的定义和翻折的性质求得∠EDF=90°，是定值．

解：（1）∵将∠ADC对折，折痕DE，

∴∠ADE=∠A′DE．

∵将∠BDC对折，折痕DF，

∴∠BDF=∠B′DF．

∵∠ADC=80°，

∴∠BDB′=180-∠ADC=180°-80°=100°．

∵∠BDF=∠B′DF=∠BDC，

∴∠BDF=×100°=50°；

（2）∵∠ADC+∠BDC=180°，∠A′DE=∠ADC，∠B′DF=∠BDC，

∴∠A′DE+∠B′DF=∠ADC+∠BDC，

∴∠EDF=（∠ADC+∠BDC）=×180°=90°．