题目内容
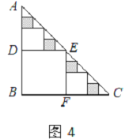
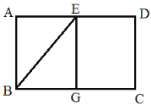
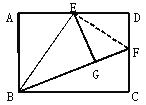
【题目】如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠,点A的对应点为点G.
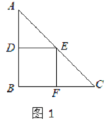
(1)填空:如图1,当点G恰好在BC边上时,四边形ABGE的形状是___________形;
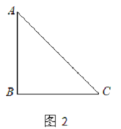
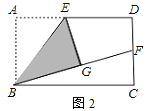
(2)如图2,当点G在矩形ABCD内部时,延长BG交DC边于点F.
![]() 求证:BF=AB+DF;
求证:BF=AB+DF;
![]() 若AD=
若AD=![]() AB,试探索线段DF与FC的数量关系.
AB,试探索线段DF与FC的数量关系.
【答案】正方形
【解析】
(1)如图1,当点G恰好在BC边上时,四边形ABGE的形状是正方形,理由为:由折叠得到两对边相等,三个角为直角,确定出四边形ABEG为矩形,再由矩形对边相等,等量代换得到四条边相等,即邻边相等,即可得证;
(2)①如图2,连接EF,由ABCD为矩形,得到两组对边相等,四个角为直角,再由E为AD中点,得到AE=DE,由折叠的性质得到BG=AB,EG=AE=ED,且∠EGB=∠A=90°,利用HL得到直角三角形EFG与直角△EDF全等,利用全等三角形对应边相等得到DF=FG,由BF=BG+GF,等量代换即可得证;
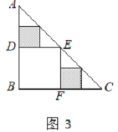
②CF=DF,理由为:不妨假设AB=DC=a,DF=b,表示出AD=BC,由①得:BF=AB+DF,进而表示出BF,CF,在直角△BCF中,利用勾股定理列出关系式,整理得到a=2b,由CD-DF=FC,代换即可得证.
(1)正方形;
(2)①如图2,连结EF,
在矩形ABCD中,AB=DC,AD=BC,∠A=∠C=∠D=90°,
∵E是AD的中点,
∴AE=DE,
∵△ABE沿BE折叠后得到△GBE,
∴BG=AB,EG=AE=ED,∠A=∠BGE=90°
∴∠EGF=∠D=90°,
在Rt△EGF和Rt△EDF中,
∵EG=ED,EF=EF,
∴Rt△EGF≌Rt△EDF,
∴ DF=FG,
∴ BF=BG+GF=AB+DF;
②不妨假设AB=DC=![]() ,DF=
,DF=![]() ,
,
∴AD=BC=![]() ,
,
由①得:BF=AB+DF
∴BF=![]() ,CF=
,CF=![]() ,
,
在Rt△BCF中,由勾股定理得:
![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即:CD=
,即:CD=![]() DF,
DF,
∵CF=![]() DF-DF,
DF-DF,
∴3CF=DF.

 天天练口算系列答案
天天练口算系列答案