题目内容
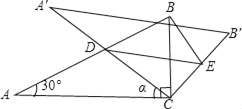
【题目】在△ABC中,∠A=60°,∠C=75°,AB=8,D、E、F分别在AB、BC、CA上,则△DEF的周长最小值是____________.
【答案】![]()
【解析】
分别作点E关于AB,AC的对称点P,Q,连结AE,AP,AQ,DP,FQ,PQ,根据两点之间线段最短以及垂线段最短,即可得出△DEF周长的最小值.
解:分别作点E关于AB,AC的对称点P,Q,连结AE,AP,AQ,DP,FQ,PQ,
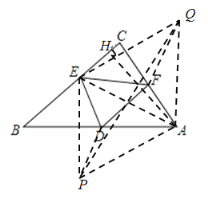
则DE=PD,EF=FQ,∠PAQ=2∠BAC=120°,且AP=AE=AQ,
∴∠APQ=30°,∴PQ=![]() AP.
AP.
过点A作AH⊥BC于点H,又∠B=180°-∠BAC-∠C=45°,
∴AH=ABsinB=8×sin45°=4![]() ,
,
△DEF的周长=DE+DF+EF=PD+DF+FQ≥PQ=![]() AP=
AP=![]() AE≥
AE≥![]() AH=4
AH=4![]() .
.
∴△DEF周长的最小值为4![]() .
.
故答案为:4![]() .
.

练习册系列答案
相关题目