题目内容
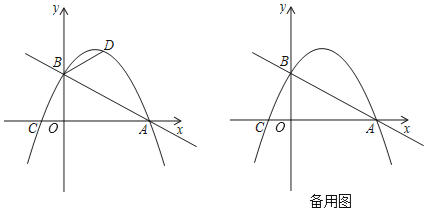
【题目】如图,已知二次函数![]() 的图像经过点
的图像经过点![]() ,顶点为
,顶点为![]() 一次函数
一次函数 ![]() 的图像交
的图像交![]() 轴于点
轴于点![]() 是抛物线上-一点,点
是抛物线上-一点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在抛物线的对称轴直线
恰好落在抛物线的对称轴直线![]() 上(对称轴直线
上(对称轴直线![]() 与
与![]() 轴交于点
轴交于点![]() ).
).
(1)求二次函数的表达式;
(2)求点![]() 的坐标;
的坐标;
(3)若点![]() 是第二象限内抛物线上一点,
是第二象限内抛物线上一点,![]() 关于抛物线的对称轴的对称点是
关于抛物线的对称轴的对称点是![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 是坐标平面内一点,若四边形
是坐标平面内一点,若四边形![]() 是正方形,求点
是正方形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点P的坐标为:(2,6)或(
;(2)点P的坐标为:(2,6)或(![]() ,
,![]() );(3)点G的坐标为:(
);(3)点G的坐标为:(![]() ,6).
,6).
【解析】
(1)直接把点A代入解析式,即可求出解析式;
(2)由题意,设点N的坐标为(![]() ,n),连接MN,过点A作AD⊥MN,AD交抛物线与点P,则点D为(
,n),连接MN,过点A作AD⊥MN,AD交抛物线与点P,则点D为(![]() ,
,![]() ),由AD⊥MN,则
),由AD⊥MN,则![]() ,求出n的值,然后求出直线AD的解析式,联合抛物线得到方程组,即可求出点P的坐标;
,求出n的值,然后求出直线AD的解析式,联合抛物线得到方程组,即可求出点P的坐标;
(3)由题意,设点G为(![]() ,
,![]() ),然后得到点E的坐标和直线OG的解析式,由点F在线段OG上,得到点F的坐标,再结合正方形的性质,有
),然后得到点E的坐标和直线OG的解析式,由点F在线段OG上,得到点F的坐标,再结合正方形的性质,有![]() ,分别求出BF、BE、EF,联立方程组,求出p的值,即可得到点G的坐标.
,分别求出BF、BE、EF,联立方程组,求出p的值,即可得到点G的坐标.
解:(1)∵二次函数![]() 的图像经过点
的图像经过点![]() ,
,
∴![]() ,
,
解得:![]() ;
;
∴二次函数的解析式为:![]() .
.
(2)由(1)知,![]() ,
,
∴顶点B为(![]() ,
,![]() ),
),
∴对称轴为![]() ;
;
在一次函数![]() 中,
中,
令![]() ,则
,则![]() ,
,
∴点M的坐标为(0,2),
设点N的坐标为(![]() ,n),
,n),
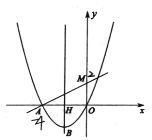
连接MN,过点A作AD⊥MN,AD交抛物线与点P,如图:
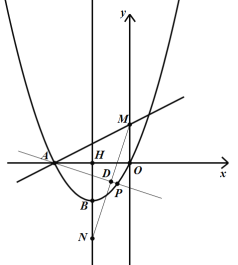
∵点M、N关于直线AP对称,
则AD垂直平分MN,即点D是MN的中点,
∴点D的坐标为(![]() ,
,![]() ),
),
∵![]() ,
,
∴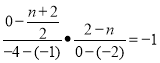 ,
,
∴![]() ,
,
解得:![]() ,
,
∴点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
结合点A(![]() ,0),可求得:
,0),可求得:
直线AD的解析式为:![]() 或
或![]() ;
;
∵抛物线的解析式为![]() ,
,
联合直线AD和抛物线,得
∴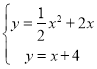 或
或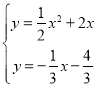 ,
,
解得: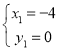 ,
,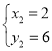 或
或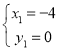 ,
,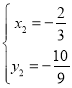 ;
;
∵点A的坐标为(![]() ,0),
,0),
∴点P的坐标为:(2,6)或(![]() ,
,![]() );
);
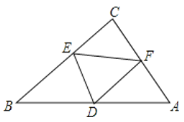
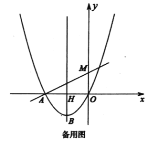
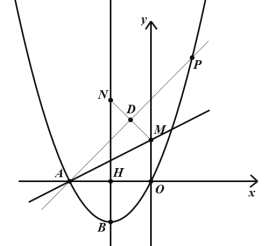
(3)由题意可知,点G在第二象限,且点G在抛物线上,四边形BDEF是正方形,连接BE、DF,如图:
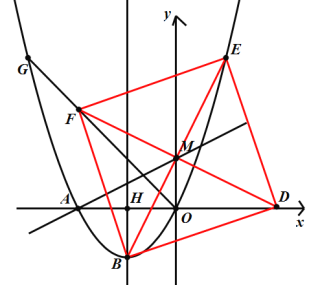
设点G为(p,![]() ),
),
∵点G与点E关于![]() 对称,
对称,
∴点E为(![]() ,
,![]() );
);
设直线OG为![]() ,则
,则
![]() ,则
,则![]() ,
,
∴直线OG为![]() ;
;
∵点F在线段OG上,则
设点F为(![]() ,
,![]() ),点F在第二象限,
),点F在第二象限,
∵四边形BDEF是正方形,
∴![]() ,
,
∵点B为(![]() ,
,![]() ),
),
∴![]() ,
,
![]() ,
,
![]() ,
,
联合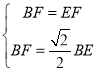 ,
,
可解得:![]() 或
或![]() ,
,
∵点F在第二象限,则![]() ,
,
∴![]() ;
;
∴![]()
∴点G的坐标为:(![]() ,6).
,6).

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
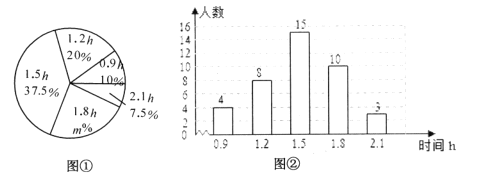
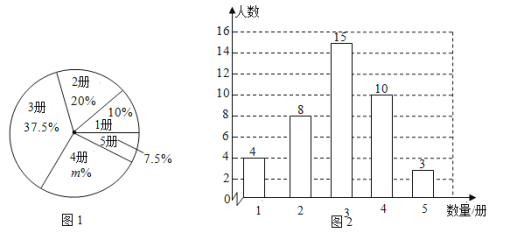
启东小题作业本系列答案【题目】某社区招募了40位居民参加“众志成城,抗击疫情”志愿者服务活动,对志愿者一天的服务时长进行调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
频数分布表
组别 | 时间/小时 | 频数/人数 |
A组 | 0≤ | 2 |
B组 | 1≤ | m |
C组 | 2≤ | 10 |
D组 | 3≤ | 12 |
E组 | 4≤ | 7 |
F组 |
| 4 |
扇形统计图
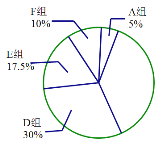
请根据图表中的信息解答下列问题:
(1)求频数分布表中的![]() 的值;
的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角的度数,并补全扇形统计图;
(3)已知F组的志愿者中,只有1名女志愿者.要从该组中选取两名志愿者分发生活物资,请用树状图或列表的方法求2名志愿恰好都是男士的概率.