题目内容
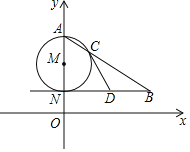
【题目】一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
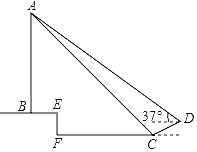
A.10.2B.9.8C.11.2D.10.8
【答案】B
【解析】
如图,作![]() 交
交![]() 的延长线于
的延长线于![]() ,延长
,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() .设
.设![]() ,在
,在![]() 中,根据
中,根据![]() ,构造方程解决问题即可.
,构造方程解决问题即可.
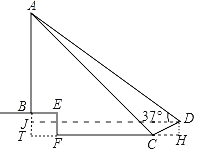
解:如图,作DH⊥FC交FC的延长线于H,延长AB交CF的延长线于T,作DJ⊥AT于J.
由题意四边形EFTB四边形DHTJ是矩形,
∴BT=EF=1.4米,JT=DH,
在Rt△DCH中,∵CD=2.6米,![]() =
=![]() ,
,
∴DH=1(米),CH=2.4(米),
∵∠ACT=45°,∠T=90°,
∴AT=TC,
设AT=TC=x.则DJ=TH=(x+2.4)米,AJ=(x﹣1)米,
在Rt△ADJ中,∵tan∠ADJ=![]() =0.75,
=0.75,
∴![]() =0.75,
=0.75,
解得x=2,
∴AB=AT﹣BT=AT﹣EF=11.2﹣1.4=9.8(米),
故选:B.

 口算题卡北京妇女儿童出版社系列答案
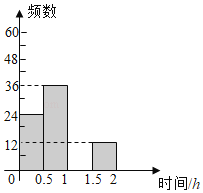
口算题卡北京妇女儿童出版社系列答案【题目】扬州市“五个一百工程“在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布表和频数分布直方图.
每天课外阅读时间t/h | 频数 | 频率 |
0<t≤0.5 | 24 | |
0.5<t≤1 | 36 | 0.3 |
1<t≤1.5 | 0.4 | |
1.5<t≤2 | 12 | b |
合计 | a | 1 |
根据以上信息,回答下列问题:
(1)表中a= ,b= ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生每天课外阅读时间超过1小时的人数.
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:

b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.