题目内容
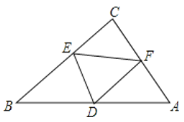
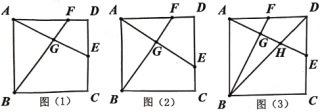
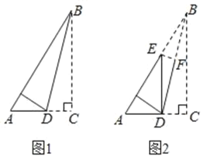
【题目】已知直角三角形纸片的两直角边AC与BC的比为3:4,首先将△ABC如图1所示折叠,使点C落在AB上,折痕为BD,然后将△ABD如图2所示折叠,使点B与点D重合,折痕为EF,则sin∠DEA的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
设AC=3x,BC=4x,由勾股定理可求AB=5x,由折叠的性质可得∠AED=2∠ABD=∠ABC,即可求sin∠DEA的值.
解:∵AC与BC的比为3:4,
∴设AC=3x,BC=4x,
∴AB=![]() =5x
=5x
∵将△ABC如图1所示折叠,使点C落在AB上,
∴∠DBC=∠DBA=![]() ∠ABC,
∠ABC,
∵将△ABD如图2所示折叠,使点B与点D重合,
∴∠ABD=∠BDE
∴∠AED=2∠ABD=∠ABC
∴sin∠DEA=sin∠ABC=![]()
故选:A.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】某社区招募了40位居民参加“众志成城,抗击疫情”志愿者服务活动,对志愿者一天的服务时长进行调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
频数分布表
组别 | 时间/小时 | 频数/人数 |
A组 | 0≤ | 2 |
B组 | 1≤ | m |
C组 | 2≤ | 10 |
D组 | 3≤ | 12 |
E组 | 4≤ | 7 |
F组 |
| 4 |
扇形统计图
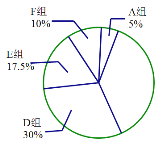
请根据图表中的信息解答下列问题:
(1)求频数分布表中的![]() 的值;
的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角的度数,并补全扇形统计图;
(3)已知F组的志愿者中,只有1名女志愿者.要从该组中选取两名志愿者分发生活物资,请用树状图或列表的方法求2名志愿恰好都是男士的概率.