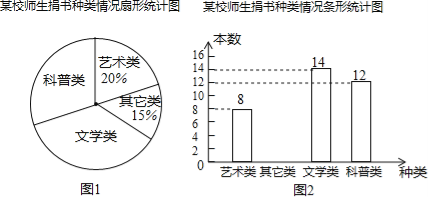
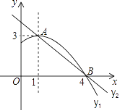
��Ŀ����
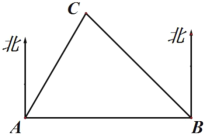
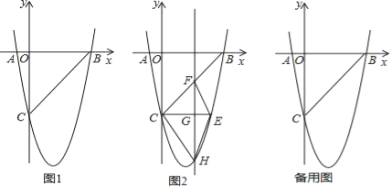
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪������y=ax2+bx-5��x�ύ��A��-1��0����B��5��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
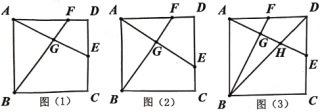
��2����ͼ2��CE��x�����������ཻ�ڵ�E����H��ֱ��CE�·��������ϵĶ��㣬����H����y��ƽ�е�ֱ����BC��CE�ֱ��ڵ�F��G����̽������H�˶����δ�ʱ���ı���CHEF�����������H�����꼰��������
��3������KΪ�����ߵĶ��㣬��M��4��m���Ǹ��������ϵ�һ�㣬��x�ᣬy�����Ƿ���ڵ�P��Q��ʹ�ı���PQKM���ܳ���С����û�У�˵�����ɣ����У������P��Q�����꣮
���𰸡���1��y=x2-4x-5����2��H��![]() ��
��![]() ����������Ϊ
����������Ϊ![]() ����3�����ڣ�P��
����3�����ڣ�P��![]() ,0����Q��0��-
,0����Q��0��-![]() ����
����
��������
��1�����ݴ���ϵ����ֱ����������߽���ʽ���ɣ�
��2����H��t��t2��4t��5�������ֱ��BC�Ľ���ʽ�����ɱ�ʾ����F�����꣬��������ı���CHEF�������t�ĺ�����ϵʽ�����ö��κ�������ֵ���ɣ�
��3�����öԳ����ҳ���P��Q��λ�ã��������P��Q�����꣮
�⣺��1���ߵ�A����1��0����B��5��0����������y��ax2+bx��5�ϣ�
��![]() ��
��
���![]() ��
��
�������ߵı���ʽΪy��x2��4x��5��
��2����H��t��t2��4t��5����
��CE��x�ᣬ
���E����������5��
��E���������ϣ�
��x2��4x��5����5��
��x��0���ᣩ��x��4��
��E��4����5����
��CE��4��
��ֱ��BC�Ľ���ʽΪy=kx��c
��B��5��0����C��0����5�����룬��
![]()
��ã�![]()
��ֱ��BC�Ľ���ʽΪy��x��5��
��F��t��t��5����
��HF��t��5����t2��4t��5��������t��![]() ��2+
��2+![]() ��
��
��CE��x�ᣬHF��y�ᣬ
��CE��HF��
��S�ı���CHEF��![]() CEHF����2��t��
CEHF����2��t��![]() ��2+
��2+![]() ��
��
��-2��0
�൱t=![]() ʱ��S�ı���CHEF������ֵΪ
ʱ��S�ı���CHEF������ֵΪ![]()
��H��![]() ����
����![]() ����
����
��3����ͼ2���ı���PQKM���ܳ�=PM��PQ��QK��KM������KMΪ��ֵ��
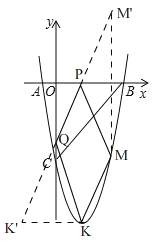
��KΪ�����ߵĶ��㣬y=x2-4x-5=��x-2��2-9
��K��2����9����
��K����y��ĶԳƵ�K������2����9����
��M��4��m�����������ϣ�
��m=16��16��5=-5
��M��4����5����
���M����x��ĶԳƵ�M����4��5����
����K��M�����ֱ�x���ڵ�P����y���ڵ�Q
���ʱPM=PM����QK=QK��
���ʱ�ı���PQKM���ܳ�=PM��PQ��QK��KM= PM����PQ ��QK����KM=M��K����KM����������֮���߶���̣���ʱ�ı���PQKM���ܳ���С
��ֱ��K��M���Ľ���ʽΪy��ex��d
��K����M����������룬��
![]()
��ã�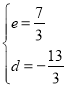
��ֱ��K��M���Ľ���ʽΪy��![]() ��
��
��y=0ʱ�����x=![]() ����x=0ʱ�����y=
����x=0ʱ�����y=![]()
��P��![]() ��0����Q��0����
��0����Q��0����![]() ����
����

����Ŀ��ij������ļ��40λ����μ�����־�ɳǣ�����������־Ը�߷�������־Ը��һ��ķ���ʱ�����е��飬�ɵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
Ƶ���ֲ���
��� | ʱ��/Сʱ | Ƶ��/���� |
A�� | 0�� | 2 |
B�� | 1�� | m |
C�� | 2�� | 10 |
D�� | 3�� | 12 |
E�� | 4�� | 7 |
F�� |
| 4 |
����ͳ��ͼ
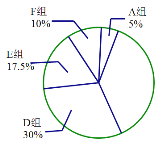
�����ͼ���е���Ϣ����������⣺
��1����Ƶ���ֲ����е�![]() ��ֵ��
��ֵ��
��2����B�飬C��������ͳ��ͼ�зֱ��Ӧ���ε�Բ�ĽǵĶ���������ȫ����ͳ��ͼ��
��3����֪F���־Ը���У�ֻ��1��Ů־Ը�ߣ�Ҫ�Ӹ�����ѡȡ����־Ը�߷ַ��������ʣ�������״ͼ���б��ķ�����2��־Ըǡ�ö�����ʿ�ĸ��ʣ�