ЬтФПФкШн
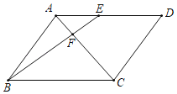
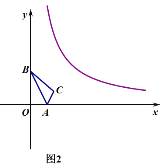
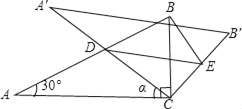
ЁОЬтФПЁПШчЭМЃЌНЋКЌ30ЁуНЧЕФжБНЧШ§НЧАхABCЃЈЁЯAЃН30ЁуЃЉШЦЦфжБНЧЖЅЕуCЫГЪБеыа§зЊІСНЧЃЈ0ЁуЃМІСЃМ90ЁуЃЉЃЌЕУЕНRtЁїAЁфBЁфCЃЌAЁфCгыABНЛгкЕуDЃЌЙ§ЕуDзїDEЁЮAЁфBЁфНЛCBЁфгкЕуEЃЌСЌНгBEЃЎвзжЊЃЌдка§зЊЙ§ГЬжаЃЌЁїBDEЮЊжБНЧШ§НЧаЮЃЎЩшBCЃН1ЃЌADЃНxЃЌЁїBDEЕФУцЛ§ЮЊSЃЎ
ЃЈ1ЃЉЕБІСЃН30ЁуЪБЃЌЧѓxЕФжЕЃЎ
ЃЈ2ЃЉЧѓSгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉвдЕуEЮЊдВаФЃЌBEЮЊАыОЖзїЁбEЃЌЕБSЃН![]() ЪБЃЌХаЖЯЁбEгыAЁфCЕФЮЛжУЙиЯЕЃЌВЂЧѓЯргІЕФtanІСжЕЃЎ
ЪБЃЌХаЖЯЁбEгыAЁфCЕФЮЛжУЙиЯЕЃЌВЂЧѓЯргІЕФtanІСжЕЃЎ
ЁОД№АИЁП(1)x=1;(2)S= ![]() ;(3)
;(3)![]()
ЁОНтЮіЁП
(1)ИљОнЕШбќШ§НЧаЮЕФХаЖЈ, ЁЯAЃНЁЯaЃН30ЁуЃЌЕУГі xЃН1.(2)гЩжБНЧШ§НЧаЮЕФаджЪ,AB=2,AC=![]() ,гЩа§зЊаджЪЧѓЕУЁїADCЁзЁїBEC,ИљОнБШР§ЙиЯЕЪН,ЧѓГіSгыxЕФКЏЪ§ЙиЯЕЪН.(3)ЕБsЃН
,гЩа§зЊаджЪЧѓЕУЁїADCЁзЁїBEC,ИљОнБШР§ЙиЯЕЪН,ЧѓГіSгыxЕФКЏЪ§ЙиЯЕЪН.(3)ЕБsЃН![]() sЁїABCЪБ,ЧѓЕУxЕФжЕ,ХаЖЯЁбEКЭDEЕФГЄЖШДѓаЁ,ШЗЖЈЁбEгыAЁфCЕФЮЛжУЙиЯЕ,дйЧѓtanІСжЕ.
sЁїABCЪБ,ЧѓЕУxЕФжЕ,ХаЖЯЁбEКЭDEЕФГЄЖШДѓаЁ,ШЗЖЈЁбEгыAЁфCЕФЮЛжУЙиЯЕ,дйЧѓtanІСжЕ.
НтЃКЃЈ1ЃЉЁпЁЯAЃНЁЯaЃН30ЁуЃЌ
гжЁпЁЯACBЃН90ЁуЃЌ
ЁрЁЯABCЃНЁЯBCDЃН60ЁуЃЎ
ЁрADЃНBDЃНBCЃН1ЃЎ
ЁрxЃН1ЃЛ
ЃЈ2ЃЉЁпЁЯDBEЃН90ЁуЃЌЁЯABCЃН60ЁуЃЌ
ЁрЁЯAЃНЁЯCBEЃН30ЁуЃЎ
ЁрACЃН![]() BCЃН
BCЃН![]() ЃЌABЃН2BCЃН2ЃЎ
ЃЌABЃН2BCЃН2ЃЎ
гЩа§зЊаджЪПЩжЊЃКACЃНAЁфCЃЌBCЃНBЁфCЃЌ
ЁЯACDЃНЁЯBCEЃЌ
ЁрЁїADCЁзЁїBECЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрBEЃН![]() xЃЎ
xЃЎ
ЁпBDЃН2ЉxЃЌ
ЁрsЃН![]() ЁС
ЁС![]() xЃЈ2ЉxЃЉЃНЉ
xЃЈ2ЉxЃЉЃНЉ![]() x2+
x2+![]() xЃЎЃЈ0ЃМxЃМ2ЃЉ
xЃЎЃЈ0ЃМxЃМ2ЃЉ
ЃЈ3ЃЉЁпsЃН![]() sЁїABC
sЁїABC
ЁрЉ![]() +
+![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр4x2Љ8x+3ЃН0ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЂйЕБxЃН![]() ЪБЃЌBDЃН2Љ
ЪБЃЌBDЃН2Љ![]() ЃН
ЃН![]() ЃЌBEЃН
ЃЌBEЃН![]() ЁС
ЁС![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁрDEЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁпDEЁЮAЁфBЁфЃЌ
ЁрЁЯEDCЃНЁЯAЁфЃНЁЯAЃН30ЁуЃЎ
ЁрECЃН![]() DEЃН
DEЃН![]()
![]() ЃОBEЃЌ
ЃОBEЃЌ
ЁрДЫЪБЁбEгыAЁфCЯрРыЃЎ
Й§DзїDFЁЭACгкFЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ ЃЈ12ЗжЃЉ
ЃЎ ЃЈ12ЗжЃЉ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрДЫЪБЁбEгыA'CЯрНЛЃЎ
ЭЌРэПЩЧѓГі ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ