Question

【题目】如图，在矩形ABCD中，已知AB=2 ，AD=2，点P是对角线BD上一动点（不与B，D重合），连接AP，过点P作PE⊥AP，交DC于点E，

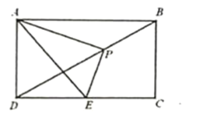
（1）求证：∠PAD=∠PEC；

（2）当点P是BD的中点时，求DE的值；

（3）在点P运动过程中，当DE= 时，求BP的值．

Answer 1

【答案】（1）见解析；（2）（3）

【解析】

（1）利用四边形的内角和和三角形外角的性质得∠DEP+∠DAP=180°，∠DEP+∠PEC=180°，再利用同角的补角相等可得结论；

（2）连接AC，交BD于P．先利用特殊角的三角函数值求出∠ADB=60°，再利用对角线的性质可得PA=PD，故△ADP为等边三角形，则AP=AD=2；然后易证Rt△ADE≌Rt△APE，可得∠DAE=∠PAE=30°，进而在Rt△ADE中利用tan∠DAE的正切求解即可；

(3)作PG⊥AB于G，GP的延长线交DC于H，得四边形ADGH是矩形，PG⊥DC，则GH＝BC＝2；设PG＝a，则PH＝GH﹣PH＝2﹣a，在Rt△BGP中利用tan∠PBG表示出BG和AG；然后易证△AGP∽△PHE，利用相似三角形的对应边成比例列出关于a比例方程并求解，即可利用BP=2PG=2a计算即可．

解：（1）证明：∵PE⊥AP，

∴∠APE=90°,

∵四边形ABCD是矩形，

∴∠ADC=90°，

在四边形ADEP中∠ADE+∠DEP+∠APE+∠DAP=360°，

∴∠DEP+∠DAP=360°-90°-90°=180°，

又∵∠DEP+∠PEC=180°，

∴∠PAD=∠PEC；

（2）解：∵四边形ABCD是矩形，AB=，AD=2，

∴，

∴∠BDA=60°，

连接AC，

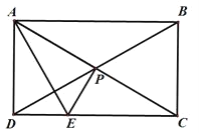
∵点P是BD的中点，

∴点P为AC与BD的交点，

∴△ADP为等边三角形，

∴AP=AD=2，

在Rt△ADE和Rt△APE中，

∴Rt△ADE≌Rt△APE（HL），

∴∠DAE=∠PAE=30°，

∴，

∴ ；

（3）解：如图，过点P作PG⊥AB于G，GP的延长线交DC于H，四边形ABCD是矩形，

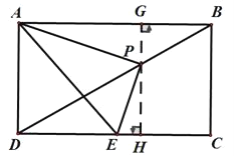
∴PG⊥DC，

∴GH＝BC＝2，

设PG＝a，则PH＝GH﹣PH＝2﹣a，

在Rt△BGP中，tan∠PBG＝，

∴BG＝PG＝a，

∴AG＝AB-BG＝2-a＝（2-a），

EH=DH-DE=2-a-=-a，

∵PG⊥DC，

∴∠APG+∠EPH＝90°，

∵∠APG+∠PAG＝90°，

∴∠EPH＝∠PAG，

∵∠AGP＝∠PHE＝90°，

∴△AGP∽△PHE，

∴，

∴，

∴

∴BP=2PG=．