Question

【题目】如图，已知△ABC内接于⊙O，AB是直径，OD⊥BC于点D，延长DO交⊙O于F，连接OC，AF．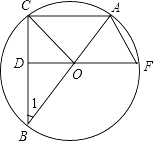
（1）求证：△COD≌△BOD；
（2）填空：①当∠1=时，四边形OCAF是菱形； ②当∠1=时，AB=2 OD．

Answer 1

【答案】
（1）证明：

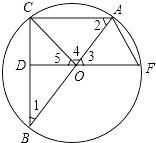
∵AF=OC=OF=AO，

∴△AOF为等边三角形，

∴∠3=60°，且∠3=∠DOB=60°，

又∵OD⊥BC，

∴D是BC的中点，∠1=30°；

∵AB是直径，

∴∠ACB=90°，

∴∠2=60°，

∴△AOC是等边三角形，

∵△AOF是等边三角形，

∴AF=OC=OF=AO，

在△AOC和△OAF中， ，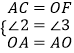

∴△AOC≌△AOF（SAS）；

（2）30°；45°
【解析】（2）解：
当∠1=30°时，四边形OCAF是菱形．
理由如下：
∵∠1=30°，AB是直径，
∴∠BCA=90°，
∴∠2=60°，而OC=OA，
∴△OAC是等边三角形，
∴OA=OC=CA，
又∵D，O分别是BC，BA的中点，
∴DO∥CA，
∴∠2=∠3=60°而OC=OA=AF．
∴△OAF是等边三角形，
∴AF=OA=OF，
∴OC=CA=AF=OF，
∴四边形OCAF是菱形；
②当∠1=45°时，AB=2 OD，
∵∠1=45°，
∵OD⊥BC于点D，
∴△BOD是等腰直角三角形，
∴OB= OD，
∴AB=2OB=2 OD．
【考点精析】根据题目的已知条件，利用菱形的判定方法和垂径定理的相关知识可以得到问题的答案，需要掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．