Question

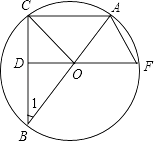
【题目】如图已知△CAB和△CDE中，CA=CB，CD=CE，∠BCA=∠DCE=.连BE，BD.

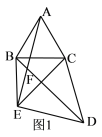
（1）如图1，若∠BCA=60，BD与AE交于点F，求∠AFB的度数；

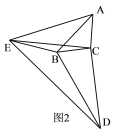
（2）如图2，请探究∠EBD，∠AEB与之间的关系；

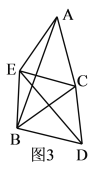
（3）如图3，直接写出∠EBD，∠AEB与之间的关系.

Answer 1

【答案】（1）60；（2）∠EBD-∠AEB=；（3）∠EBD+∠AEB+=360.

【解析】

（1）∠ACE=∠ACB+∠BCE=∠DCE+∠BCE=∠BCD，再由AC=BC和CE=CD可证明△ACE≌BCD，则∠CAE=∠CBD，由图可知∠CAE+∠ACB=∠CBD+∠BFA，则∠AFB=∠ACB=60°；

（2）由AC=BC，EC=DC且∠ACE=∠α-∠ECB=∠BCD，易证△ACE≌BCD，则∠AEC=∠BDC，再由∠EBD=∠CEB+∠CDB+∠ECD可得

∠EBD=∠AEB+∠ECD=∠AEB+，则∠EBD-∠AEB=；

（3）同上易证△ACE≌BCD，从而∠CAE=∠CBD，由四边形ECDB的内角和定理可得∠CEB+∠CBD+∠ECD+∠BDC=360°，则∠EBD+∠AEB+=360.

（1）∵∠ACE=∠ACB+∠BCE，∠BCD=∠DCE+∠BCE，

∴∠ACE=∠BCD，

又∵AC=BC，CE=CD，

∴△ACE≌BCD，

∴∠CAE=∠CBD，

∵∠CAE+∠ACB=∠CBD+∠BFA，

∴∠AFB=∠ACB=60°.

（2）∠EBD-∠AEB=.

证明：

∵∠ACE=∠ACB-∠BCE，∠BCD=∠DCE-∠BCE，

∴∠ACE=∠BCD，

又∵AC=BC，CE=CD，

∴△ACE≌BCD，

∴∠AEC=∠BDC，

∵∠EBD=∠CEB+∠CDB+∠ECD，

∴∠EBD=∠AEB+∠ECD=∠AEB+，

即∠EBD-∠AEB=.

（3）∠EBD+∠AEB+=360.

∵∠ACE=∠ACB-∠BCE，∠BCD=∠DCE-∠BCE，

∴∠ACE=∠BCD，

又∵AC=BC，CE=CD，

∴△ACE≌BCD，

∴∠CAE=∠CBD，

在四边形ECDB中，

∵∠CEB+∠CBD+∠ECD+∠BDC=360°，

∴∠EBD+∠AEB+=360.