Question

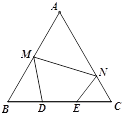
【题目】如图，等边△ABC的边长为12，D，E为BC的三等分点，M，N分别为AB，AC上的动点，则四边形DENM周长的最小值是_________.

Answer 1

【答案】20

【解析】

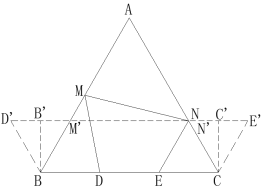
作D点关于AB的对称点D’、E点关于AC的对称点E’，连接D’E’分别与AB和AC交于M’和N’，则当M点运动至M’点、N点运动至N’点时，DM+MN+NE的最小值为D’E’，此时四边形DMNE的周长最小；分别作CC’⊥D’E’、BB’⊥D’E’，由对称及等边△ABC易知△N’CE’和△BM’D’均为等边三角形，由此可求解出D’E’的长度，进而求解四边形的周长.

解：作E点关于AC的对称点E’，过E’点作BC的平行线交AC于N’、交AB于M’，在直线E’M’上取D’点，连接BD’使BD’=BD，则当M点运动至M’点、N点运动至N’点时，DM+MN+NE的最小值为D’E’，此时四边形DMNE的周长最小；

由对称性可知，∠N’CE=∠N’CE’=60°，

∵E’N’∥BC，

∴∠E’N’C=∠N’CE=∠N’CE’=60°,

∴△N’E’C是等边三角形，

∵E’D’∥BC，CE’=BD’，

∴四边形BCE’D’是等腰梯形，

∴∠D’=60°，

∵E’N’∥BC，

∴∠D’M’B=∠M’BD=60°，

∴△D’M’B是等边三角形，

分别作CC’⊥D’E’、BB’⊥D’E’，由图可知，D’E’长度等于BC长度再加上△N’E’C(或△D’M’B)的边长，则D’E’=12+4=16，

则四边形DENM周长的最小值=16+4=20.

故答案为：20.