Question

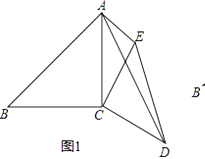
【题目】已知等腰直角△ABC，∠C＝90°，点D是斜边AB的中点，E是AC上的动点、∠EDF＝90°，DF交BC 于点F．

（1）当 DE⊥AC，DF⊥BC 时，（如图1），我们很容易得出：S△DEF+S△CEF=S△ABC.

（2）如图2，DE与 AC不垂直，且点E在线段AC上时，（1）中的结论是否成立，如果不成立，请说明理由；如果成立，请证明．

（3）当点E运动到AC延长线上，其他条件不变，请把图3补充完整，直接写出 S△DEF，S△CEF，S△ABC的关系．

Answer 1

【答案】（1）证明见解析；（2）成立；证明见解析；（3）S△DEF﹣S△CEF＝S△ABC．

【解析】

（1）根据三角形的中位线和正方形的性质即可得到结论；

(2)如图 2，过 D作 DM⊥AC于 M，DN⊥BC于 N，根据三角形的中位线大小在得到 DM＝DN，推出四边形 CNDM是正方形，得到 S正方形 DMCN＝S△ABC， 根据余角的性质得到∠EDM＝∠FDN，根据全等三角形的性质得到△EDM≌△FDN，于是得到结论；

(2)如图 3，过 D作 DM⊥AC于 M，DN⊥BC于 N，根据三角形的中位线大小在得到DM＝DN，推出四边形 CNDM是正方形，得到 S正方形 DMCN＝S△ABC，根据余角的性质得到∠EDM＝∠FDN，根据全等三角形的性质得到△EDM≌△FDN，于是得到结论．

（1）∵DE⊥AC，DF⊥BC，

∴DE∥BC，DF∥AC，

∵点D是斜边AB的中点，AC＝BC，

∴DE＝DF＝AC，

∴EF＝AB，

∴S△DEF+S△CEF＝S四边形 DECF＝S△ABC；

（2）结论仍然成立，

证明：如图2，过D作DM⊥AC于M，DN⊥BC于N，

∴∠AMC＝∠DNC＝∠C＝90°，

∴DM∥BC，DN∥AC，

∵点D是斜边AB的中点，

∴DM＝BC，DN＝AC，

∴DM＝DN，

∴四边形CNDM是正方形，

∴S正方形DMCN＝S△ABC，

∵∠EDF＝90°，

∴∠EDM＝∠FDN，

在△EDM与△FDN中，

∴△EDM≌△FDN，（ASA），

∴S四边形CFDE＝S正方形DMCN＝S△DEF+S△CEF＝S△ABC；

（3）如图3，

过D作DM⊥AC于M，DN⊥BC于N，

∴∠AMC＝∠DNC＝∠C＝90°，

∴DM∥BC，DN∥AC，

∵点D是斜边AB的中点，

∴DM＝BC，DN＝AC，

∴DM＝DN，

∴四边形CNDM是正方形，

∴S正方形DMCN＝S△ABC，

∵∠EDF＝90°，

∴∠EDM＝∠FDN，

在△EDM与△FDN中， ，

∴△EDM≌△FDN，（ASA），

∴S四边形CFDE＝S正方形DMCN＝S△DEF﹣S△CEF＝S△ABC．