Question

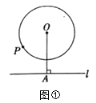
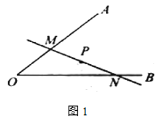
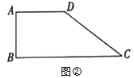
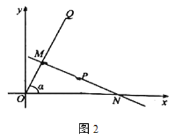
【题目】定义：如图1，已知锐角内有定点，过点任意作一条直线，分别交射线，于点M，N．若是线段的中点时，则称直线是的中点直线．如图2，射线的解析式为与轴的夹角为，，为的中点直线．

（1）求直线的解析式；

（2）若过点任意作一条直线，分别交射线，轴的正半轴于点，，记的面积为，的面积为．求证：．

Answer 1

【答案】（1）直线MN的解析式为；（2）见解析．

【解析】

（1）设点M的坐标为，分别过点M、N作x轴的垂线，利用∽，求出，得到点M的坐标，再利用待定系数法求直线MN解析式即可；

（2）设，过点作轴交于，根据轴，点P是线段MN的中点可证得≌，进而得到即可求证．

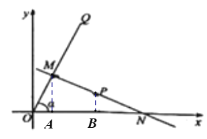
（1）解：如图，设点的坐标为，

作轴，轴，垂足分别为，，

∴，

∴∽，

∴．

∵点是线段的中点，P(3，1)，

∴PB=1，

∴，即，解得．

∴点M的坐标为（1，2），

设直线的解析式为，

把，；，代入，

得，解得，

∴中点直线的解析式为．

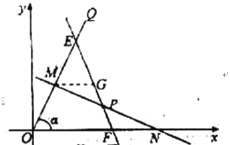
（2）证明：如图，不妨设，过点作轴交于．

则有，．

∵是的中点，∴，∴≌．

∴，∴．

∵，∴，

当与重合时，．

∴．