题目内容
【题目】如图是水平放置的水管截面示意图,已知水管的半径为50cm,水面宽AB=80cm,则水深CD约为______cm.

【答案】20
【解析】
连接OA,设CD为x,由于C点为弧AB的中点,CD⊥AB,根据垂径定理的推理和垂径定理得到CD必过圆心0,即点O、D、C共线,AD=BD=![]() AB=40,在Rt△OAD中,利用勾股定理得(50-x)2+402=502,然后解方程即可.
AB=40,在Rt△OAD中,利用勾股定理得(50-x)2+402=502,然后解方程即可.
解:连接OA、如图,设⊙O的半径为R,
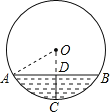
∵CD为水深,即C点为弧AB的中点,CD⊥AB,
∴CD必过圆心O,即点O、D、C共线,AD=BD=![]() AB=40,
AB=40,
在Rt△OAD中,OA=50,OD=50-x,AD=40,
∵OD2+AD2=OA2,
∴(50-x)2+402=502,解得x=20,
即水深CD约为为20.
故答案为;20

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】以下是某市自来水价格调整表(部分):(单位:元/立方米)
用水类别 | 现行水价 | 拟调整水价 |
一、居民生活用水 | 0.72 | |
1、一户一表 | ||
第一阶梯:月用水量0~30立方米/户 | 0.82 | |
第二阶梯:月用水量超过30立方米/户部分 | 1.23 |
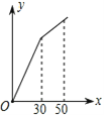
则调整水价后某户居民月用水量x(立方米)与应交水费y(元)的函数图象是( )
A. B.
B. C.
C. D.
D.