Question

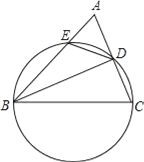
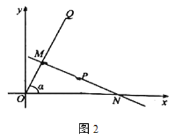
【题目】如图，在正方形ABCD中，AB＝16．连接AC，点P在线段AC上，PA＝AC，作射线PM与边AB相交于点E．将射线PM绕点P逆时针旋转90°得到射线PN，射线PN与边BC相交于点F．当△AEP的面积为时．在边CD上取一点G．则△AFG周长的最小值是_____．

Answer 1

【答案】

【解析】

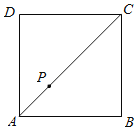
如图，作点Ｆ关于点C的对称点H，连接AH，GH，过点P作PK⊥BC于K，PJ⊥AB于J．利用三角形的面积公式求出AE，再利用相似三角形的性质求出KF，利用勾股定理求出AF，AH，GH+AG+GF的最小值即可解决问题．

解：如图，作点F关于点C的对称点H，连接AH，GH，过点P作PK⊥BC于K，PJ⊥AB于J．

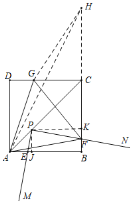
∵四边形ABCD是正方形，AB＝16，

∴AC＝AB＝16，

∵PA＝AC，

∴PA＝4，

∵PJ⊥AJ，∠PAJ＝45°，

∴PJ＝AJ＝4，BJ＝16﹣4＝12，

∵PK⊥BC，

∴∠B＝∠PJB＝∠PKB＝90°，

∴四边形PJBK是矩形，

∴PK＝BJ＝12，

∵S△PAE＝＝AEPJ，

∴AE＝，EJ＝4﹣＝，

∵∠JPK＝∠MPN＝90°，

∴∠JPE＝∠FPK，

∵∠PJE＝∠PKF＝90°，

∴△PJE∽△PKF，

∴，

∴，

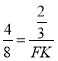∴FK＝，CF＝12+＝，BF＝，

∴BH＝＝，

∴AF＝＝＝，AH＝＝＝，

∵GF＝GH，

∴AG+FG＝AG+GH，

∵AG+GH≥AH，

∴AG+GH≥，

∴GA+FG的最小值为，

∴△AFG的周长的最小值为+．

故答案为：．