题目内容
【题目】如图,已知![]() ,以
,以![]() 为直径的
为直径的![]() 交边
交边![]() 于点
于点![]() ,
,![]() 与
与![]() 相切.
相切.
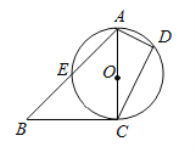
(1)若![]() ,求证:
,求证:![]() ;
;
(2)点![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 两点在
两点在![]() 的异侧.若
的异侧.若![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接CE,依据题意和圆周角定理求得△ABC是等腰直角三角形,然后根据圆周角定理和等腰三角形三线合一的性质求解即可;
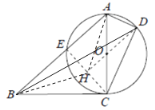
(2)连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,根据圆周角定理结合已知条件可得
,根据圆周角定理结合已知条件可得![]() ,从而判定
,从而判定![]() ,得到
,得到![]() ,从而根据垂径定理可得EH=CH,根据三角形中位线定理可求
,从而根据垂径定理可得EH=CH,根据三角形中位线定理可求![]() ,然后设圆的半径为r,根据勾股定理列方程即可求出r,从而求出EH,然后根据相似三角形的判定及性质求出AB,再根据平行线的距离处处相等可得
,然后设圆的半径为r,根据勾股定理列方程即可求出r,从而求出EH,然后根据相似三角形的判定及性质求出AB,再根据平行线的距离处处相等可得![]() ,从而求出结论.
,从而求出结论.
(1)证明:连接![]() .
.
![]() 为
为![]() 的直径,
的直径,![]() 与
与![]() 相切,
相切,
![]() ,
,
![]() ,
,
![]() ,
,
∴△ABC是等腰直角三角形,
![]() ,
,
![]() .
.
(2)连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() 为直径,
为直径,
![]() ,
,
![]() ,
,
![]() 为
为![]() 中点.
中点.
![]() ,
,
![]()
设![]() 的半径为
的半径为![]()
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]()
解得![]() 或
或![]() (舍去)
(舍去)
![]() ,
,
由勾股定理得![]()
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]()
解得![]() .
.
![]() ,
,
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】绘制函数![]() 的图象,我们经历了如下过程:确定自变量
的图象,我们经历了如下过程:确定自变量![]() 的取值范围是
的取值范围是![]() ;列表-描点--连线,得到该函数的图象如图所示
;列表-描点--连线,得到该函数的图象如图所示
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
观察函数图象,回答下列问题:
(1)函数图象在第 象限;
(2)函数图象的对称性是
B.只是轴对称图形,不是中心对称图形
A.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
C.不是轴对称图形,而是中心对称图形
(3)在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
在![]() 时,当
时,当![]() 时,函数
时,函数![]() 有最 (大,小)值,且这个最值等于
有最 (大,小)值,且这个最值等于
(4)方程![]() 是否有实数解?说明
是否有实数解?说明