题目内容
如图,在矩形ABCD中,AB=3cm,BC=4cm.设P、Q分别为BD、BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q的移动时间为t(0<t≤4)

小题1:求△PBQ的面积S(cm2)与时间t(s)之间的函数关系式;
小题2:是否存在时刻t,使△PBQ的面积与四边形CDPQ的面积相等?若有,请求出时间t的
值;若没有,请说明理由;
小题3:当t为何值时,△PBQ为等腰三角形?并判断△PBQ能否
成为等边三角形?

小题1:求△PBQ的面积S(cm2)与时间t(s)之间的函数关系式;
小题2:是否存在时刻t,使△PBQ的面积与四边形CDPQ的面积相等?若有,请求出时间t的
值;若没有,请说明理由;
小题3:当t为何值时,△PBQ为等腰三角形?并判断△PBQ能否
成为等边三角形?
小题1:
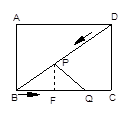
∵矩形ABCD中,AB=3cm,BC=4cm
∴CD= AB=3cm
∴在Rt△BCD中 BD="5cm"
由题意得:PD=t,BQ=t,BP=5-t
过P作PE⊥BC于E,则PE∥CD
∴△BPE∽△BDC ∴
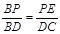 即
即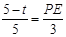
∴
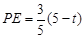 2分
2分∴
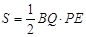
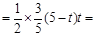
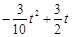 3分
3分小题2:不存在t满足条件
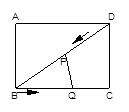
∵
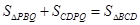 ∴
∴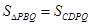 时,有
时,有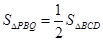
∵
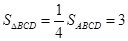
∴令
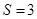 ,则有
,则有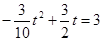 即
即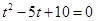 5分
5分∵
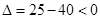 ∴方程无实数根
∴方程无实数根∴不存在满足条件的t 6分
小题3:若BP="PQ " 则过P作PF⊥BC于F
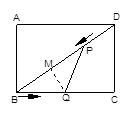
∴PF∥CD BF=QF=
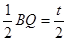
∴△BPF∽△BDC ∴
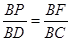
即
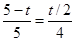 ∴
∴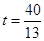
若BP=QB,则
 ∴
∴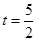
若QB=PQ,则过Q作QM⊥BD于M
∴∠BMQ=∠C=90° BM=PM=
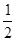 BP
BP∵∠CBD=∠CBD ∴△BMQ∽△BDC
∴
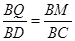 即
即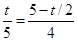 ∴
∴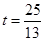
∴
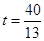 ,
,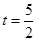 ,
,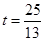 时,△PBQ为等腰三角形 9分
时,△PBQ为等腰三角形 9分△PBQ不能为等边三角形 10分
略

练习册系列答案
相关题目



 ,则它的两条对角线的长分别为___________
,则它的两条对角线的长分别为___________