题目内容
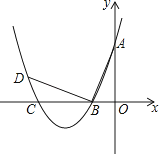
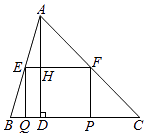
【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3 ![]() ﹣3,CD∥AB,并与弧AB相交于点M、N.
﹣3,CD∥AB,并与弧AB相交于点M、N. 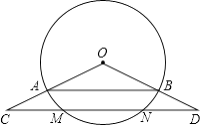
(1)求线段OD的长;
(2)若sin∠C= ![]() ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度.
【答案】
(1)解:∵OA=OB∴∠OAB=∠OBA
∵CD∥AB∴∠OAB=∠C,∠D=∠OBA
∴∠C=∠D,
∴OD=OC=OA+AC=3 ![]() ;
;
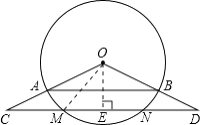
(2)解:过O作OE⊥CD,连接OM,则ME= ![]() MN,
MN,
∵tan∠C= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴设OE=x,则CE=2x,
在Rt△OEC中,OC2=OE2+CE2,即(3 ![]() )2=x2+(2x)2,解得x=
)2=x2+(2x)2,解得x= ![]()
在Rt△OME中,OM2=OE2+ME2,即32=( ![]() )2+ME2,解得ME=
)2+ME2,解得ME= ![]() ,
,
∴由垂径定理得MN=3;
(3)解:由(2)可得△OMN是等边三角形,
∴∠MON=60°
∴优弧MEN的长度= ![]() =5π.
=5π.
【解析】(1)根据CD∥AB,OA=OB,推出∠C=∠D,根据等腰三角形的判定证得OD=OC即可;(2)过O作OE⊥CD,连接OM,由垂径定理可知ME= ![]() MN,再根据tan∠C=
MN,再根据tan∠C= ![]() 可求出OE的长,利用勾股定理即可求出ME的长,进而求出答案;(3)由(2)可得△OMN是等边三角形,即∠MON=60°,由弧长公式即可得到结论.
可求出OE的长,利用勾股定理即可求出ME的长,进而求出答案;(3)由(2)可得△OMN是等边三角形,即∠MON=60°,由弧长公式即可得到结论.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案【题目】近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
学生对使用计算器影响计算能力发展的看法统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数 | 100 | 60 | m |
根据以上图表信息,解答下列问题: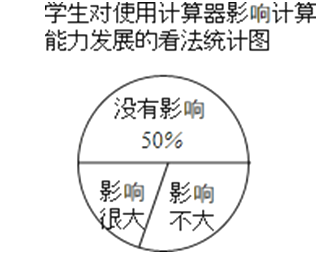
(1)统计表中的m= ;
(2)统计图中表示“影响不大”的扇形的圆心角度数为 度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?