题目内容
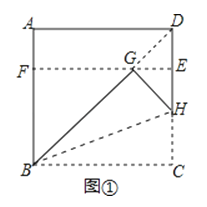
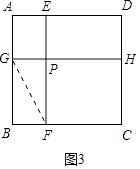
【题目】如图边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形,EF与GH交于点P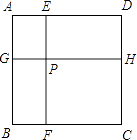
(1)若AG=AE,证明:AF=AH;
(2)若矩形PFCH的面积,恰矩形AGPE面积的两倍,试确定∠HAF的大小;
(3)若矩形EPHD的面积为 ![]() ,求Rt△GBF的周长.
,求Rt△GBF的周长.
【答案】
(1)
解:证明:如图1中,连接AF、AH,
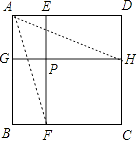
由题意知四边形AGHD与四边形AEFB均为矩形,
∴AG=DH,AE=BF,
∵AG=AE,
∴DH=BF,
∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ADH与Rt△ABF中,
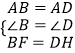 ,
,
∴△ABF≌△ADH,
∴AF=AH;
(2)
解:结论:∠HAF=45°.
理由:设AG=a,BG=b,AE=x,ED=y.
则 ![]() ,
,
∴a﹣x=y﹣b,两边平方得a2﹣2ax+x2=y2﹣2yb+b2,
∴得a2﹣2ax+x2=y2﹣4ax+b2,
∴(a+x)2=y2+b2,
∵y2+b2=FH2,
∴a+x=FH,
∵AG=DH=a,AE=BF=x,
∴DH+BF=FH,
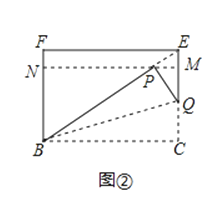
延长FB到M,使得BM=DH,连接AM,
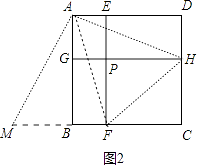
∵AD=AB,∠D=∠ABM,DH=BM,
∴△ADH≌△ABM,
∴AH=AM,∠DAH=∠BAM,
∴∠MAH=∠BAD=90°,
∵AF=AF,AM=AH,FM=FH,
∴△AFM≌△AFH,
∴∠FAH=∠FAM=45°
(3)
解:如图3中,连接GF,设BC=x,BF=y,则FG= ![]() ,
,
∴(x﹣1)(y﹣1)= ![]() ,∴xy﹣x﹣y+1=
,∴xy﹣x﹣y+1= ![]() ,∴xy﹣x﹣y=﹣
,∴xy﹣x﹣y=﹣ ![]()
∴x2+y2=x2+y2+1+2xy﹣2x﹣2y,
∴ ![]() =1﹣x﹣y,
=1﹣x﹣y,
得x+y+ ![]() =1,
=1,
∴Rt△GBF的周长=1.
【解析】(1)如图1中,连接AF、AH,由题意知四边形AGHD与四边形AEFB均为矩形,只要证明△ABF≌△ADH即可.(2)结论:∠HAF=45°.设AG=a,BG=b,AE=x,ED=y.由 ![]() ,推出(a+x)2=y2+b2 , 由y2+b2=FH2 , 推出a+x=FH,由AG=DH=a,AE=BF=x,推出DH+BF=FH,延长FB到M,使得BM=DH,连接AM,只要证明△ADH≌△ABM即可解决问题.(3)如图3中,连接GF,设BC=x,BF=y,则FG=
,推出(a+x)2=y2+b2 , 由y2+b2=FH2 , 推出a+x=FH,由AG=DH=a,AE=BF=x,推出DH+BF=FH,延长FB到M,使得BM=DH,连接AM,只要证明△ADH≌△ABM即可解决问题.(3)如图3中,连接GF,设BC=x,BF=y,则FG= ![]() ,由(x﹣1)(y﹣1)=
,由(x﹣1)(y﹣1)= ![]() ,推出xy﹣x﹣y+1=
,推出xy﹣x﹣y+1= ![]() ,推出xy﹣x﹣y=﹣
,推出xy﹣x﹣y=﹣ ![]() 推出x2+y2=x2+y2+1+2xy﹣2x﹣2y,推出
推出x2+y2=x2+y2+1+2xy﹣2x﹣2y,推出 ![]() =1﹣x﹣y,得x+y+
=1﹣x﹣y,得x+y+ ![]() =1,延长即可解决问题.
=1,延长即可解决问题.
【考点精析】通过灵活运用矩形的性质和正方形的性质,掌握矩形的四个角都是直角,矩形的对角线相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案