Question

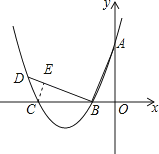
【题目】如图，在平面直角坐标系中．顶点为（﹣4，﹣1）的抛物线交y轴于点A（0，3），交x轴于B，C两点．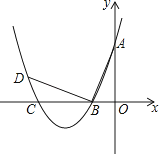

（1）求此抛物线的解析式；
（2）已知点P是抛物线上位于B，C两点之间的一个动点，问：当点P运动到什么位置时，四边形ABPC的面积最大？并求出此时四边形ABPC的面积．
（3）过点B作AB的垂线交抛物线于点D，是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆？若存在，求出圆的半径；若不存在，请说明理由．

Answer 1

【答案】
（1）

【解答】解：根据题意，可设抛物线的解析式为y=a（x+4）2﹣1，

把点A（0，3）代入得：3=16a﹣1，

解得a=，

所以此抛物线的解析式为y=（x+4）2﹣1；

（2）

令y=0，则0=（x+4）2﹣1；

解得x1=﹣2，x2=﹣6，

∴B（﹣2，0），C（﹣6，0），

∴BC=4，

∵S四边形ABPC=S△ABC+S△PBC，S△ABC=BCOA=×4×3=6，

∴要使四边形ABPC的面积最大，则△PBC的面积最大，

∴当P点移动到抛物线的顶点时△PBC的面积最大，

∴四边形ABPC的面积的最大值为：S△ABC+S△PBC=6+×4×1=6+2=8；

（3）

如图，设⊙C与BD相切于点E，连接CE，则∠BEC=∠AOB=90°．

∵A（0，3）、B（﹣2，0）、C（﹣6，0），

∴OA=3，OB=2，OC=6，BC=4；

∴AB==，

∵AB⊥BD，

∴∠ABC=∠EBC+90°=∠OAB+90°，

∴∠EBC=∠OAB，

∴△OAB∽△EBC，

∴，即

∴EC=．

设抛物线对称轴交x轴于F．

∵抛物线的对称轴x=﹣4，

∴CF=2≠，

∴不存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆．

【解析】