��Ŀ����
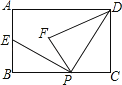
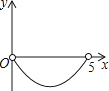
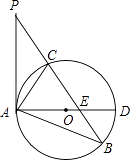
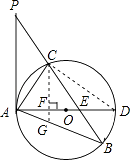
����Ŀ����֪���κ���y=ax2+bx+c��a��0��������M����1��2���͵�N��1����2������x����A��B���㣬��y����C����
��a+c=0��
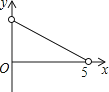
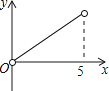
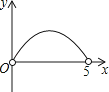
������aȡ��ֵ���˶��κ���ͼ����x������������㣬����ͼ���x�����õ��߶γ��ȱش���2��
�۵�������x�� ![]() ʱ��y��x���������С��
ʱ��y��x���������С��
�ܵ���1��m��n��0ʱ��m+n�� ![]() ��
��
����a=1����OAOB=OC2 ��
����˵����ȷ���У� ��
A.�٢ڢۢܢ�
B.�٢ڢܢ�
C.�ڢۢ�
D.�٢ڢۢ�
���𰸡�B
���������⣺�߶��κ���y=ax2+bx+c��a��0��������M����1��2���͵�N��1����2����
�� ![]() ��
��
���+�ڵã�a+c=0���ʢ���ȷ��
��a=��c
��b2��4ac��0��
������aȡ��ֵ���˶��κ���ͼ����x������������㣬
��|x1��x2|= ![]() =
= ![]() ��
�� ![]() =��1��
=��1��
�� ![]() ��2��
��2��
�ʢ���ȷ��
���κ���y=ax2+bx+c��a��0���ĶԳ���x=�� ![]() =
= ![]() ����a��0ʱ�����ж�x��
����a��0ʱ�����ж�x�� ![]() ʱ��y��x���������С���ʢ۴���
ʱ��y��x���������С���ʢ۴���
�ߩ�1��m��n��0��a��0��
��m+n��0�� ![]() ��0��
��0��
��m+n�� ![]() ������ȷ��
������ȷ��
��a=1��
����κ���Ϊy=x2+bx+c��
��OC2=c2=|x1x2|=OAOB������ȷ��
��ӦѡB��

��ϰ��ϵ�д�
�����Ŀ