题目内容
【题目】阅读理解
抛物线y=
x2上任意一点到点（0，1）的距离与到直线y=﹣1的距离相等，你可以利用这一性质解决问题．
问题解决
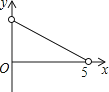
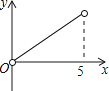
如图，在平面直角坐标系中，直线y=kx+1与y轴交于C点，与函数y=x2的图象交于A，B两点，分别过A，B两点作直线y=﹣1的垂线，交于E，F两点．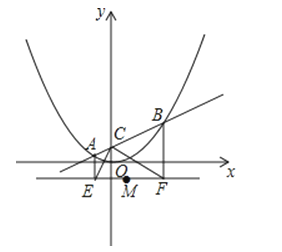
（1）写出点C的坐标，并说明∠ECF=90°
（2）在△PEF中，M为EF中点，P为动点．
①求证：PE2+PF2=2（PM2+EM2）；
②已知PE=PF=3，以EF为一条对角线作平行四边形CEDF，若1＜PD＜2，试求CP的取值范围．
【答案】
（1）
解：当x=0时，y=k0+1=1，
则点C的坐标为（0，1）．
根据题意可得：AC=AE，
∴∠AEC=∠ACE．
∵AE⊥EF，CO⊥EF，
∴AE∥CO，
∴∠AEC=∠OCE，
∴∠ACE=∠OCE．
同理可得：∠OCF=∠BCF．
∵∠ACE+∠OCE+∠OCF+∠BCF=180°，
∴2∠OCE+2∠OCF=180°，
∴∠OCE+∠OCF=90°，即∠ECF=90°
（2）
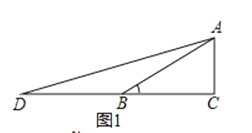
①过点P作PH⊥EF于H，
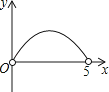
Ⅰ．若点H在线段EF上，如图2①．
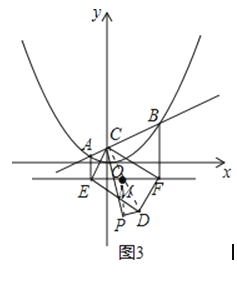
∵M为EF中点，
∴EM=FM=
EF．
根据勾股定理可得：
PE2+PF2﹣2PM2=PH2+EH2+PH2+HF2﹣2PM2
=2PH2+EH2+HF2﹣2（PH2+MH2）
=EH2﹣MH2+HF2﹣MH2
=（EH+MH）（EH﹣MH）+（HF+MH）（HF﹣MH）
=EM（EH+MH）+MF（HF﹣MH）
=EM（EH+MH）+EM（HF﹣MH）
=EM（EH+MH+HF﹣MH）
=EMEF=2EM2，
∴PE2+PF2=2（PM2+EM2）；
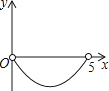
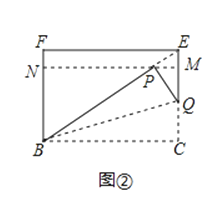
Ⅱ．若点H在线段EF的延长线（或反向延长线）上，如图2②．
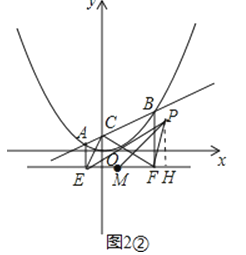
同理可得：PE2+PF2=2（PM2+EM2）．
综上所述：当点H在直线EF上时，都有PE2+PF2=2（PM2+EM2）；
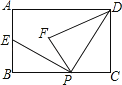
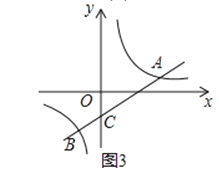
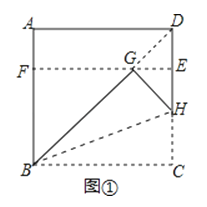
②连接CD、PM，如图3．
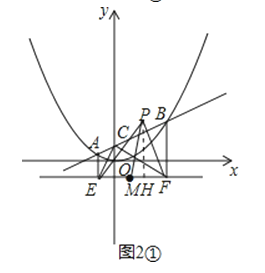
∵∠ECF=90°，
∴CEDF是矩形，
∵M是EF的中点，
∴M是CD的中点，且MC=EM．
由①中的结论可得：
在△PEF中，有PE2+PF2=2（PM2+EM2），
在△PCD中，有PC2+PD2=2（PM2+CM2）．
∵MC=EM，
∴PC2+PD2=PE2+PF2．
∵PE=PF=3，
∴PC2+PD2=18．
∵1＜PD＜2，
∴1＜PD2＜4，
∴1＜18﹣PC2＜4，
∴14＜PC2＜17．
∵PC＞0，
∴
＜PC＜
．
【解析】（1）如图1，只需令x=0，即可得到点C的坐标．根据题意可得AC=AE，从而有∠AEC=∠ACE．易证AE∥CO，从而有∠AEC=∠OCE，即可得到∠ACE=∠OCE，同理可得∠OCF=∠BCF，然后利用平角的定义即可证到∠ECF=90°；
（2））①过点P作PH⊥EF于H，分点H在线段EF上（如图2①）和点H在线段EF的延长线（或反向延长线）上（如图2②）两种情况讨论，然后只需运用勾股定理及平方差公式即可证到PE2+PF2﹣2PM2=2EM2 ， 即PE2+PF2=2（PM2+EM2）；
②连接CD，PM，如图3．易证CEDF是矩形，从而得到M是CD的中点，且MC=EM，然后根据①中的结论，可得：在△PEF中，有PE2+PF2=2（PM2+EM2），在△PCD中，有PC2+PD2=2（PM2+CM2）．由MC=EM可得PC2+PD2=PE2+PF2 ． 根据PE=PF=3可求得PC2+PD2=18．根据1＜PD＜2可得1＜PD2＜4，即1＜18﹣PC2＜4，从而可求出PC的取值范围．
【考点精析】认真审题，首先需要了解二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)，还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键．
