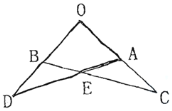
题目内容
【题目】已知抛物线y=a(x-2)2-9经过点P(6,7),与x轴交于A、B两点,与y轴交于点C,直线AP与y轴交于点D,抛物线对称轴与x轴交于点E.
(1)求抛物线的解析式;
(2)过点E任作一条直线l(点B、C分别位于直线l的异侧),设点C到直线的距离为m,点B到直线l的距离为n,求m+n的最大值;
(3)y轴上是否存在点Q,使∠QPD=∠DEO,若存在,请求出点Q的坐标:若不存在,请说明理由.
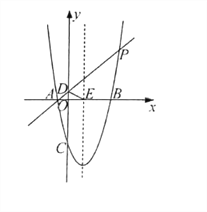
【答案】(1) y=x2-4x-5;(2)![]() ;(3)Q1(0,5),Q2(0,-11).
;(3)Q1(0,5),Q2(0,-11).
【解析】分析:(1)把P点坐标代入y=a(x-2)2-9中求出a即可得到抛物线解析式;
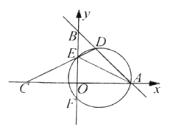
(2)作BM⊥l于M,BN⊥l于N,BG⊥CM于G,如图1,利用四边形BGMN为矩形得到BN=MG,则m+n=CG,利用BG≤BC(当且仅当M点在BC上取等号)得到m+n的最大值为BC的长,然后求出B、C坐标后计算出BC即可;
(3)先利用待定系数法求出直线AD的解析式为y=x+1,则D(0,1),PD=6![]() ,△AOD为等腰直角三角形,易得E(2,0),则tan∠DEO=
,△AOD为等腰直角三角形,易得E(2,0),则tan∠DEO=![]() ,讨论:当点Q在点D的上方,作QG⊥AP于G,如图2,设QG=t,证明△QDG为等腰直角三角形得到DG=QG=t,QD=
,讨论:当点Q在点D的上方,作QG⊥AP于G,如图2,设QG=t,证明△QDG为等腰直角三角形得到DG=QG=t,QD=![]() t,则利用∠QPD=∠DEO和正切定义得到
t,则利用∠QPD=∠DEO和正切定义得到![]() ,解方程求出t,从而可确定Q点坐标;当点Q在点D的下方,作QG⊥AP于G,如图3,设QG=t,利用同样方法得到
,解方程求出t,从而可确定Q点坐标;当点Q在点D的下方,作QG⊥AP于G,如图3,设QG=t,利用同样方法得到![]() ,然后解方程求出t,从而得到Q点坐标.
,然后解方程求出t,从而得到Q点坐标.
详解:(1)∵抛物线y=a(x-2)2-9经过点P(6,7),
∴a(6-2)2-9=7,解得a=1,
∴抛物线解析式为y=(x-2)2-9,
即y=x2-4x-5;
(2)作BM⊥l于M,BN⊥l于N,BG⊥CM于G,如图1,
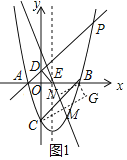
易得四边形BGMN为矩形,
∴BN=MG,
∴m+n=CM+BN=CM+MG=CG,
∵BG≤BC(当且仅当M点在BC上取等号)
∴m+n的最大值为BC的长,
当x=0时,y=x2-4x-5=-5,则C(0,-5),
当y=0时,x2-4x+5=0,解得x1=-1,x2=5,则A(-1,0),B(5,0)
∴BC=![]() ,
,
∴m+n的最大值为5![]() ;
;
(3)存在.
设直线AD的解析式为y=kx+b,
把A(-1,0),P(6,7)代入得![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+1,
当x=0,y=x+1=1,则D(0,1),
∴PD=![]() ,△AOD为等腰直角三角形,
,△AOD为等腰直角三角形,
∵抛物线的对称轴为直线x=2,
∴E(2,0),
∴tan∠DEO=![]() ,
,
当点Q在点D的上方,作QG⊥AP于G,如图2,
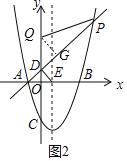
设QG=t,
∵∠QDG=∠ADO=45°,
∴△QDG为等腰直角三角形,
∴DG=QG=t,QD=![]() QG=
QG=![]() t,
t,
∴PG=PD-DG=6![]() -t,
-t,
∵∠QPD=∠DEO,
∴tan∠QPD=![]() ,
,
∴![]() ,解得t=2
,解得t=2![]() ,
,
∴DQ=2![]() ×
×![]() =4,
=4,
∴OQ=4+1=5,
∴Q点坐标为(0,5);
当点Q在点D的下方,作QG⊥AP于G,如图3,
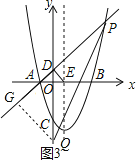
设QG=t,
∴△QDG为等腰直角三角形,
∴DG=QG=t,QD=![]() QG=
QG=![]() t,
t,
∴PG=PD+DG=6![]() +t,
+t,
∵∠QPD=∠DEO,
∴tan∠QPD=![]() ,
,
∴![]() ,解得t=6
,解得t=6![]() ,
,
∴DQ=6![]() ×
×![]() =12,
=12,
∴OQ=12-1=11
∴Q点坐标为(0,-11),
综上所述,Q点的坐标为(0,5)或(0,-11).