题目内容
【题目】阅读下面的证明过程,指出其错误.(在错误部分下方划线)已知△ABC,求证:∠A+∠B+∠C=180°
(1)证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(作图)
∴∠2=∠B(内错角相等两直线平行)
∵∠1=∠C(作图)
∴∠B+∠C+∠3=∠2+∠1+∠3(等量代换)
∠2+∠l+∠3=180°(周角的定义)
即∠BAC+∠B+∠C=180°(等量代换)
(2)类比探究:请同学们参考图2,模仿(1)的解决过程,避免(1)中的错误,试说明求证:∠A+∠B+∠C=180°
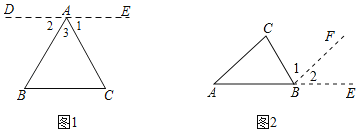
【答案】(1)见解析;(2)见解析
【解析】
(1)根据平行线的判定由DE∥BC可得∠1=∠C,所以且使∠1=∠C就多余了,∠2+∠1+∠180°(平角定义),不是周角定义.
(2)模仿(1)的证明过程即可.
解:(1)
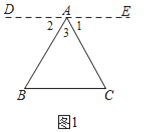
证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(作图)
∴∠2=∠B(内错角相等,两直线平行)
∵∠1=∠C(作图)
∴∠B+∠C+∠3=∠2+∠1+∠3(等量代换)
∠2+∠1+∠3=180°(周角的定义)
即∠BAC+∠B+∠C=180°(等量代换)
(2)如图2,
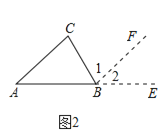
证明:延长AB到E,过点B作BF∥AC.
∵BF∥AC(作图)
∴∠1=∠C (两直线平行内错角相等)
∠2=∠A ( 两直线平行同位角相等)
∵∠2+∠1+∠ABC=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换).

练习册系列答案
相关题目